Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 2.1 - Ex. 11
Considere a função dada por
Mostre que
Esboce o gráfico de
Qual o menor valor de ? Em que este menor valor é atingido?
Passo 1
Olá pessoal, tudo bem? Vou ajudar vocês nessa questão, vamos lá?
Considerando a função dada , a fim de mostrar a igualdade da letra , podemos fazer o que eu chamo de “truque sujo”, ou a técnica de completar o quadrado.
Mas o que é isso? Bom, lembrando-se de produtos notáveis temos:
O que queremos mostrar é a equivalência de:
Certo?
Então saca só o truque sujo! Comparando as duas expressões, podemos chamar de e , não é?
Mas não faltaria um , ou melhor, um na expressão da direita? Pois aqui que mora o truque sujo! Dá uma olhada naquele dando sopa: ele não pode ser escrito como ? PODE!
E é isso que vou fazer!
É a mesma expressão que tínhamos antes, certo? E sabendo da propriedade dos produtos notáveis, podemos juntar os três primeiros termos do lado direito e escrever como :
E é exatamente isso que o problema pede pra mostrar! Eu acho um super truque sujo! Mas na verdade a técnica de transformar um polinômio em um produto notável é de “completar quadrado”, pois aqui nós reescrevemos a expressão a fim de que ela fique na forma de um quadrado perfeito =)
Beleza? Bora pra próxima?
Passo 2
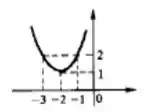
Agora o problema pede para esboçar o gráfico. Bom, a é uma função de segunda ordem, portanto a cara dela é de uma parábola. E parábola nós desenhamos a partir de quatro pontos:
As duas raízes (onde o gráfico corta o eixo );
O ponto do termo independente (onde o gráfico corta o eixo )
E o vértice: que mostra onde o gráfico vai apresentar o valor máximo (se a parábola tiver boca para baixo ) ou um mínimo (se a parábola tiver boca para cima ).
Então vamos aos pontos?
Vamos achar as raízes da função:
Usando a fórmula de Bhaskara temos:
Xiiii! Aqui temos um probleminha, o valor de é negativo, ou seja, essa função não admite raízes reais: ela está “voando”. Mas tudo bem! Temos mais dois outros pontos para determinar. Bora lá?
Agora onde a função corta o eixo vertical: :
Certo! Achamos o ponto .
Por fim, vamos ao vértice. A coordenada do vértice é então:
E a coordenada é dada por :
Perfeito! O outro ponto é . Como essa parábola tem , ela tem boca para cima, então o vértice representa o valor mínimo que ela pode assumir.
Para poder fazer um desenho mais preciso, vou determinar dois pontos em torno do vértice:
Agora sabendo todos esses pontos, podemos colocar num gráfico:
Beleza, vamos pra última parte da questão?
Passo 3
Então, aqui a questão pergunta qual o menor valor atingido pela . Em se tratando de uma parábola com boca para cima, o menor valor atingido será no ponto de abscissa e de ordenada , que já calculamos no passo anterior:
Assim o menor valor atingido será de , com .
Resposta
