Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 2.1 - Ex. 15p

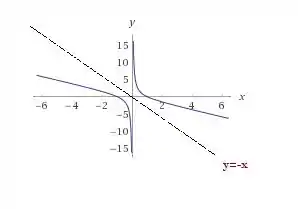
Dê o domínio e esboce o gráfico.

p ) y = - x + (1)/(x)

Passo 1

O domínio dessa função é bem tranquilo. Lembrando que não podemos ter divisão por zero, então:

D = {x in R| x != 0 }

Passo 2

Agora o esboço do gráfico. Ele vai ter cara de hipérbole, porém com aquele – x adicionado na função, o gráfico fica sendo simétrico em torno da reta y = - x .

As raízes dessa função serão:

y = 0

- x + (1)/(x) = 0

(1)/(x) = x

x^2 = 1 :. x = +- 1

Serão 1 e - 1 . E ela não corta o eixo y , pois x != 0 .

Passo 3

Com a ajuda de um programa de geração gráfica temos:

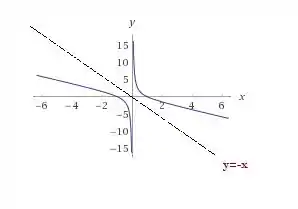
Resposta

D = {x in R| x != 0 }

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Simplifique (f (x + h) - f ( x ))/(h) ( h != 0 ) sendo f ( x ) igual al ) f (x) = x^3
Simplifique (f (x + h) - f ( x ))/(h) ( h != 0 ) sendo f ( x ) igual ad ) f (x) = x^2
Simplifique f x + h - f ( x ) h( h ≠ 0 ) sendo f ( x ) igual a e ) f x = x 2 + 3 x
Simplifique (f (x + h) - f ( x ))/(h) ( h != 0 ) sendo f ( x ) igual an ) f (x) = x^3 + x^2 - x
Simplifique (f (x + h) - f ( x ))/(h) ( h != 0 ) sendo f ( x ) igual ac ) f (x) = - 2 x + 4