Considere o objeto de massa em queda do Exemplo 2, mas suponha agora que o coeficiente de resistência do ar é proporcional ao quadrado da velocidade.
- Se a velocidade limite é (a mesma que no Exemplo 2), mostre que a equação de movimento pode ser escrita como
- Se , encontre uma expressão para em qualquer instante.
- Faça o gráfico da solução encontrada em (b) e da solução (26) do Exemplo 2 no mesmo conjunto de eixos.
- Baseado nos gráficos encontrados em (c), compare o efeito de um coeficiente de resistência do ar quadrático com um linear
- Encontre a distância percorrida pelo objeto até o instante .
- Encontre o tempo que leva para o objeto cair .
Veja também o Problema 25 da Seção 1.1
Passo 1
Para resolvermos esse problema vamos, para o primeiro item, manipular a equação que chegamos no exercício 25 da seção 1.1 para chegar na forma pedida. Para os itens restantes, vamos aplicar os diferentes tipos de condições de contorno pedidos com o intuito de encontrar os dados requisitados. Vamos juntos para resolver!!
Passo 2
- Pela equação encontrada no exercício 25 da seção 1.1, temos que
- Para encontrarmos a velocidade, precisamos resolver a EDO. Primeiramente vamos transformar ela em umaequação separável.
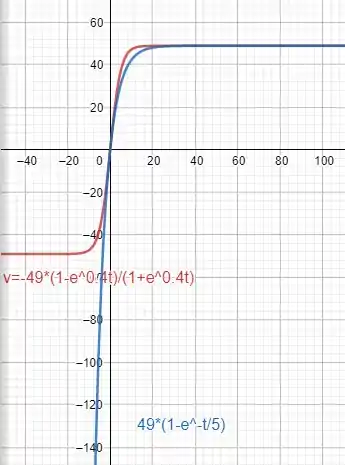
- No caso de uma resistência do ar com o quadrado da velocidade, a mesma é atingida mais rapidamente, porém, como conseguimos perceber no gráfico do item anterior, a velocidade terminal ainda será a mesma para um mesmo objeto.
- Para encontrarmos a distância percorrida, precisamos integrar novamente nossa expressão em função do tempo. Portanto, temos que:
- Para encontrarmos o tempo para essa distância, precisamos isolar e aplicar o ponto de contorno. Assim, aplicando a exponencial de ambos os lados da expressão, temos que:
Podemos escrever o valor de em uma fração equivalente, que será de aproximadamente . Assim, temos que nossa equação fica
Se somarmos esses dois valores fazendo um mínimo múltiplo comum, vamos ter que
Como queríamos chegar
Passo 3
Se integrarmos de ambos os lados, vamos chegar em
Se aplicarmos a condição de contorno com , teremos que
Assim, ficamos com
Agora vamos manipular a equação para isolar . Temos que:
Vamos aplicar a exponencial em ambos os lados, mas antes vamos nos atentar ao módulo aplicado. Como é a velocidade máximo, temos que para o termo precisamos que . Substituindo e aplicando a exponencial, temos que
Assim, temos que essa é nossa equação para em qualquer é essa
Passo 4
Passo 5
Passo 6
Integrando de ambos os lados, temos
Supondo que , temos que
Assim, nossa equação se torna
Passo 7
Usando o arccosh, temos que
Resposta
(b)
(e)
(f)