Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 8.1 - Ex. 58

Considere a região delimitada pelos gráficos de y   =   t g - 1     x , y   = 0 e x =   1 .

a. Determine a área da região.

b. Determine o volume do sólido formado pela rotação dessa região em torno do eixo das ordenadas.

Passo 1

A questão nos da duas funções y e um pontos como vemos no gráfico abaixo:

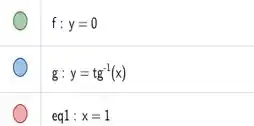
O enuciado se divide em “a” e “b”. Na letra “a” pede para determinar a área da região que é o mesmo que calcular a integral definida entre os limites do eixo x (eixo das ordenadas). Usaremos a seguinte fórmula:

A = ∫ a b f ( x ) - g ( x ) d x

Já a letra “b”nos pede o volume do sólido que é formado após a rotação da área que encontramos na letra “a”. Usaremos a fórmula do volume:

V = ∫ a b 2 π . x . f ( x )   d x

Passo 2

Para resolver a letra “a” iremos aplicar a fórmula:

A = ∫ a b f ( x ) - g ( x ) d x

Como percebemos no gráfico a função maior é y   =   t g - 1     x , ou seja, f ( x ) =   t g - 1   x . Logo, g ( x )   = 0 o que significa que ela é uma função constante e esta no eixo das ordenadas. Assim é possivel perceber que as funções se encontram na origem onde x = 0 . Entam os limites de x são:

x = 0

x =   1

Substituindo:

A = ∫ 0 1   t g - 1   x - 0 d x

A = ∫ 0 1   t g - 1   x d x

Vamos resolver essa integral por partes como se fosse indefinida para facilitar os cálculos:

u = t g - 1   x

d u = t g - 1   x ' d x

d u = 1 1 + x 2   d x

d v = 1   d x

d v = ∫ 1   d x

v = x  

∫ u   d v = u . v -   ∫ v   d u

∫   t g - 1   x   d x = t g - 1   x . x -   ∫ x .   1 1 + x 2   d x

Para simplificar ∫ x .   1 1 + x 2   d x usaremos o método da substituição:

w = 1 + x 2

d w = 1 + x 2 '   d x

d w = 2 x   d x

∫ x .   1 1 + x 2   d x

multiplicamos por um valor neutro para que possa substituir. É possível notar que 2 2 é o melhor número pois é o mesmo que multiplicar por 1

2 2 ∫ x .   1 1 + x 2   d x = 1 2 ∫ 2 x .   1 1 + x 2   d x

= 1 2 ∫   1 w   d w

= 1 2 . l n w

Substituindo w = 1 + x 2 :

= 1 2 . l n 1 + x 2

Agora substituimos na equação principal:

∫   t g - 1   x   d x = t g - 1   x . x -   ∫ x .   1 1 + x 2   d x

∫   t g - 1   x   d x = t g - 1   x . x -   1 2 . l n 1 + x 2

Por últimos aplicamos a integral definida:

∫ 0 1   t g - 1   x d x = t g - 1   x . x -   1 2 . l n 1 + x 2 0 1

= t g - 1   1 . 1 -   1 2 . l n 1 + 1 2 - t g - 1   0 . 0 -   1 2 . l n 1 + 0 2

= π 4 - l n   2 2 - 0

= π - 2 l n   2 4

Passo 3

Agora iremos fazer o cálculo do volume usando a fórmula de volume:

V = ∫ a b 2 π . x . f ( x )   d x

Como uma das funções esta no eixo das ordenadas usaremos a função maior   y   =   t g - 1     x :

V = ∫ a b 2 π . x . t g - 1     x d x

Reorganizando:

∫ a b 2 π . x . t g - 1     x   d x   = 2 π ∫ 0 1 x . t g - 1     x   d x

Para continuar desenvolvendo vamos usar integração por partes como se fosse indefinida para facilitar os cálculos:

u = t g - 1

d u = t g - 1   x '   d x

d u = 1 1 + x 2   d x

d v = x   d x

d v = ∫ x   d x

v = x 2 2

∫ u   d v = u . v -   ∫ v   d u

∫ x . t g - 1     x   d x = t g - 1 x . x 2 2 -   ∫ x 2 2 . 1 1 + x 2   d x

= t g - 1 x . x 2 2 - 1 2   ∫ x 2 . 1 1 + x 2   d x

Para continuar desenvolvendo vamos somar 0 na integral (somar 0 é somar um valor e aomesmo tempo subtrair esse valor na equação, assim seria o mesmo que somar 0, não alterando o resultado):

= t g - 1 x . x 2 2 - 1 2   ∫ x 2 + 1 - 1 1 + x 2   d x

= t g - 1 x . x 2 2 - 1 2   ∫ x 2 + 1 - 1 1 + x 2   d x

= t g - 1 x . x 2 2 - 1 2   ∫ x 2 + 1 1 + x 2   d x - ∫ 1 1 + x 2   d x

= t g - 1 x . x 2 2 - 1 2   ∫ 1   d x - ∫ 1 1 + x 2   d x

= t g - 1 x . x 2 2 - 1 2   x - t g - 1   x

= t g - 1 x . x 2 2 - x 2 + t g - 1   x 2

Aplicamos agora a integral definida:

2 π ∫ 0 1 x . t g - 1     x   d x = 2 π t g - 1 x . x 2 2 - x 2 + t g - 1   x 2 0 1

= 2 π t g - 1 1 . 1 2 2 - 1 2 + t g - 1   1 2 - 2 π t g - 1   0 . 0 2 2 - 0 2 + t g - 1   0 2

= 2 π π 8 - 1 2 + π 8 - 2 π . 0

= 2 π π 4 - 1 2

= π 2 2 - π

Resposta

a. A = π - 2 l n   2 4  

b.

V = π 2 2 - π

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ache o volume do solido de revolução descrito quando a região dada da figura for rotacionada em torno da reta indicada.Uma equação da curva na figura é y 2 = x 3 O B C em torno do eixo y
Ache o volume do solido de revolução descrito quando a região dada da figura for rotacionada em torno da reta indicada.Uma equação da curva na figura é y 2 = x 3 O B C em torno do eixo x
Ache o volume do sólido de revolução geradp éça rotação, em torno da reta indicada, da região limitada pela curva y = x , pelo eixo x e pela reta 4 .A reta x = 4
Ache o volume do solido de revolução descrito quando a região dada da figura for rotacionada em torno da reta indicada.Uma equação da curva na figura é y 2 = x 3 O B C em torno da reta A C
Ache o volume do sólido de revolução gerado pela rotação, em torno da reta indicada, da região limitada pela curva y = x , pelo eixo x e pela reta x = 4 Ao redor do eixo x