Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 6.1 - Ex. 12

Ache o volume do solido de revolução descrito quando a região dada da figura for rotacionada em torno da reta indicada.

Uma equação da curva na figura é y 2 = x 3

O B C em torno do eixo x

Passo 1

A figura que ele deu é:

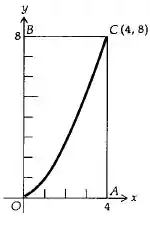
Com a curva

y 2 = x 3

Aqui, queremos o colume de O B C em torno do eixo x

Como estamos trabalhando com rotação no eixo paralelo ao x , devemos olhar o intervalo de variação nele. Vamos ter, pelo gráfico:

x = 0

x = 4

Para acharmos a função em x , já que estamos rodando paralelo ao eixo x vamos isolar o y

y 2 = x 3 → y = x 3 2

Na verdade aqui, temos duas regiões. Uma da Curva O C até o eixo x , e outra da reta B C até o eixo x .

O volume vai ser a subtração dessas duas:

V = V 1 - V 2

Onde:

da Curva O C até o eixo x → V 2

da retra B C até o eixo y → V 1

Vamos ver os raios de cada região:

r 2 x = x 3 2

Da vermelha para a verde, vamos ter:

r 1 x = 8

O volume vai ser a subtração dos dois volumes:

V = V 1 - V 2

V 1 = ∫ 0 8 π 8 2 d x = x

V 2 = ∫ 0 8 π x 3 2 2 d x = ∫ 0 8 π x 3 d x

Passo 2

Vamos resolver essas integral:

V 1 = ∫ 0 4 π 64 d x = 64 π ∫ 0 4 d x = 64 π x 0 4 = 64 π 4 - 0 = 256 π

Passo 3

Vamos para a o outro volume:

V 2 = ∫ 0 4 π x 3 d x

V 2 = π ∫ 0 4 x 3 d x

Primeiro, vamos fazer:

∫ x 3 d x = ∫ x 3 d x = x 4 4 + C

Voltando para a nossa integral definida:

V 2 = π ∫ 0 4 x 3 d x = π x 4 4 0 4 =

π 4 4 4 - π 0 4 4

π 64 =

64 π

Passo 4

Nosso volume vai ficar:

V = V 1 - V 2 = 256 π - 64 π = 192 π

Resposta

192 π

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule o volume do sólido obtido pela rotação, em torno do eixo x, do conjunto de todos os pares ( x , y ) tais queg) x 2 ≤ y ≤ x .
Calcule o volume do sólido obtido pela rotação, em torno do eixo x, do conjunto de todos os pares ( x , y ) tais que 1 ≤ x ≤ 3e0 ≤ y ≤ x
Calcule o volume do sólido obtido pela rotação, em torno do eixo x, do conjunto de todos os pares ( x , y ) tais queb) 1 2 ≤ x ≤ 2e0 ≤ y ≤ 1 x 2
Calcule o volume do sólido obtido pela rotação, em torno do eixo x, do conjunto de todos os pares ( x , y ) tais quee) y ≥ 0 ,1 ≤ x ≤ 2ex 2 - y 2 ≥ 1 .
Calcule o volume do sólido obtido pela rotação, em torno do eixo x, do conjunto de todos os pares ( x , y ) tais queh) 0 ≤ y ≤ xex 2 + y 2 ≤ 2 .