Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 8.3 - Ex. 56

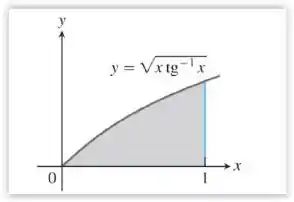
Considere a região delimitada pelos gráficos de y = xtan - 1 ⁡ x , y=0 0 para 0 ≤ x ≤ 1 . Determine o volume do sólido formado pela rotação dessa região em torno do eixo das abscissas (veja figura a seguir).

Passo 1

Fala aí, queremos encontrar o volume do sólido formado pela rotação da região. Temos que a função é y = x tan - 1 ⁡ x , e o gráfico e delimitado pelos pontos y=0 0 para 0 ≤ x ≤ 1 . Estamos diante de uma questão onde vamos precisar integrar a função dada para encontrar o volume e em seguida aplicar os limites de integração que são os pontos onde a região está delimitada.

Então, o volume é dado por:

V =   ∫ 0 1 π x tan - 1 ⁡ x 2 d x =   π ∫ 0 1 x tan - 1 ⁡ x   d x

Agora, para resolver, vamos utilizar o método da integração por partes:

∫ u   d v = u v -   ∫ v   d u

Vamos chamar u = tan - 1 ⁡ x     → d u =   1 1 + x   d x

d v = x   → v =   ∫ x   d x =   x 2 2

Passo 2

Substituindo na integral acima, temos:

= π ∫ 0 1 x tan - 1 ⁡ x   d x =   π     1 2 x 2 tan - 1 ⁡ x 1 0   - 1 2 ∫ 0 1 x 2 1 + x 2   d x

= π   (   1 2 tan - 1 ⁡ x - 0 )   - 1 2 ∫ 0 1 1 -   1 1 - x 2

= π   π 8 - 1 2 ∫ 0 1 d x + 1 2 ∫ 0 1 1 1 + x 2   d x  

= π   1 8 + - 1 2 x + 1 2 tan - 1 ⁡ x ]   1 ¦ 0  

= π   π 8 + - 1 2 + 1 2 tan - 1 ⁡ 1 + 0 - 0 )

= π ( π - 2 ) 4

Resposta

π ( π - 2 ) 4

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a integral. int (d x)/(sqrt(x^2 + 16)) d x
Calcule a integral. int (sqrt(1 + x^2))/(x) d x
Calcule a integral. int (x)/(sqrt(x^2 + x + 1)) d x
Calcule a integral. int sqrt(1 - 4 x^2) d x
Calcule a integral usando a substituição trigonométrica indicada. Esboce e coloque legendas no triângulo retângulo associado. ∫ x 3 x 2 + 9 d x ; x = 3 tg ⁡ θ