Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 7.3 - Ex. 19
Calcule a integral.
Passo 1
Olá, meu nobre amigo. Yuri aqui e estarei te ajudando a resolver essa atividade.
Aqui temos uma integral onde uma substituição ‘comum’ não funciona muito bem.
Estas integrais são trabalhosas e voc�� sempre vai precisar pensar, mas com MUITA prática você consegue e vai ver que vai conseguir pensar nas substituições só de bater o olho na integral.
Como essa aqui, uma substituição simples não funciona, então irei lhe apresentar a substituição trigonométrica.
Tenho até uma tabela para te ajudar:
O triângulo retângulo associado a esse desenho é o seguinte:
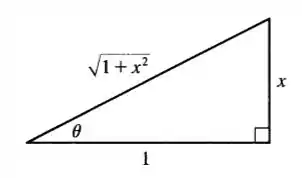
Passo 2
A gente tem que , e varia no intervalos . Assim, se fizermos a derivada de , a gente tem .
Agora, achando o valor da nossa hipotenusa por meio da substituição de , temos:
Passo 3
Assim, o valor da nossa integral é: