Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 9.3 - Ex. 17
Considere o sistema autônomo
a) Mostre o que o ponto crítico (0,0) é um ponto de sela.
b) Esboce as trajetórias para o sistema linear correspondente integrando a equação para Mostre, da forma paramétrica da solução, que a única trajetória na qual quando é .
c) Determine as trajetórias para o sistema não linear integrando a equação para Esboce as trajetórias para o sistema não linear que correspondem a e a para o sistema linear.
Passo 1
a) O a matriz jacobiana é:
Na origem o coeficiente matriciano do sistema linearizado é
Os autovalores complexo . Os autovalores são reais e com sinal oposto. Logo o ponto crítico é um ponto de sela.
Passo 2
b) As trajetórias do sistema linearizado são solução da equação diferencial
que é uma EDO separável. Integrando ambos os lados da equação , a solução é . A trajetória consiste numa da família das hipérboles.
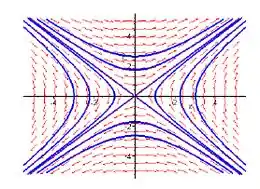
Dá pra percebermos que a solução geral vai ser dada por e . A única solução consiste naquelas que . Neste caso,
Passo 3
c) A trajetória do sistema dado são soluções da equação diferencial
que pode também ser escrito como O resutado da EDO é exato.
Integrando a primeira equação nós encontramos a equação . Isso nos da que
Comparando as derivadas parciais nós obtemos Logo as soluções são as curvas de nível da função
As trajetórias se aproximando ou divergindo da origem não são mais linhas retas.
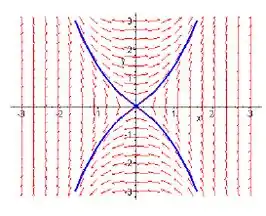
Resposta
Ei, a resposta está no passo a passo :)