Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 9.3 - Ex. 22
Considere mais uma vez as equações do pêndulo (Veja problema 21)
Se o pêndulo é colocado em movimento a partir de sua posição mais baixa de equilíbrio com velocidade angular então as condições iniciais são
a) Faça os gráficos de x em função de t para e também para Explique os movimentos diferentes do pêndulo representados por esses dois gráficos.
b)Existe um valor crítico de que denotaremos por tal que um tipo de movimento ocorre para e outro tipo ocorre para . Explique o valor de
Passo 1
a) Para
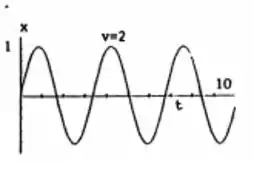
Para
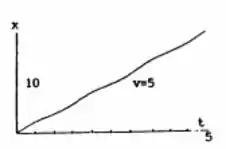
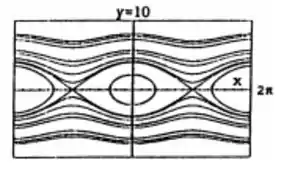
Passo 2
b) Pelos graficos do intem a nós vemos que enta entre . Usando vários valores prar , estimamos por tentativa
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Encontre os pontos críticos.
Esboce as trajetórias em uma vizinhança de cada ponto crítico. Calcule e faça o gráfico de um número suficiente de trajetórias do sistema dado de modo a mostrar, claramente, o comportamento das soluçõ
Esboce as trajetórias em uma vizinhança de cada ponto crítico. Calcule e faça o gráfico de um número suficiente de trajetórias do sistema dado de modo a mostrar, claramente, o comportamento das soluçõ
Desenhe um campo de direções e descreva como as soluções parecem se comportar.
Para cada ponto crítico, encontre o sistema linear correspondente. Encontre os autovalores e autovetores do sistema linear; classifique cada ponto crítico em relação ao tipo e determine se é assintoti