Considere o sistema autônomo
a) Mostre o que o ponto crítico (0,0) é um ponto de sela.
b) Esboce as trajetórias para o sistema linear correspondente e mostre que a trajetória na qual quando é .
c) Determine as trajetórias para o sistema não linear integrando a equação para Mostre que a trajetória correspondente a para o sistema não-linear não se altera, mas que a correspondente a é . Esboce diversas trajetórias para o sistema não-linear.
Passo 1
a) O sistema é
Aplicando no ponto critico (0,0) temos Os autovalores são reais e de sinais diferentes, logo sabemos que aorigem é um ponto de sela instável para ambos os sistemas lineares e quase linear.
Passo 2
b) A trajetória do sistema linear são soluções de
Logo temos e
Para esboçar isso resolvemos a primeira equação para e substituímos o resultado na segunda equação e obtemos , .
Várias trajetórias são mostradas na figura abaixo.
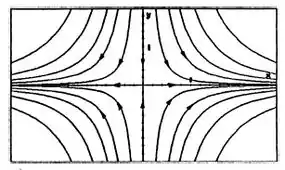
Como nós devemos escolher para
Logo é a única trajetória para o qual quando
Passo 3
c) Para nós temos
Isso é uma equação linear e a solução geral é onde é uma constante arbitrária.
O sistema de equações ainda tem a solução . Qualquer solução como ponto incial no eixo y, ou seja é dada pela última solução. As trajetórias correspondentes a essas soluções se aproximam da origem quando
A trajetória qua passa pela origem é dada por . Essa trajetória corresponde a trajetória para o problema linear. Várias trajetórias são esboçadas na figura abaixo.
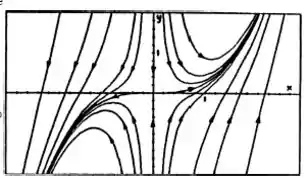
Resposta
Ei, a resposta está no passo a passo :)