Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 4.2 - Ex. 39d
Considere o sistema mola-massa ilustrado na Figura 4.2.4 consistindo em duas massas unitárias suspensas de molas com constantes 3 e 2, respectivamente. Suponha que não há amortecimento no sistema.
Observe que as soluções obtidas nos itens (c) e (d) descrevem dois modos de vibração distintos.
Passo 1
Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos pede para encontrarmos a solução da nossa equação. Parece muita coisa, mas é tranquilo. Partiu??
Passo 2
Ok, nosso primeiro passo vai ser montar o sistema:
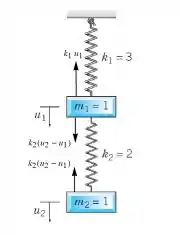
Logo, nosso sistema é:
Passo 3
Pronto!! Agora é só substituir os valores e achar a solução!!
No primeiro, a frequência do movimento é 1, e as duas massas se movem em fase,
ambas se movendo para cima ou para baixo, juntas; a segunda massa se move duas vezes mais
rápido do que a primeira. O segundo movimento tem frequência , e as massas se movem fora
de fase uma em relação à outra, uma movendose para baixo enquanto a outra se move para
cima, e vice-versa. Nesse modo, a primeira massa se move duas vezes mais rápido do que a
segunda. Para outras condições iniciais que não são proporcionais à Eq. (iii) nem à Eq. (iv), o
movimento das massas é uma combinação desses dois modos de vibração.
Resposta
No primeiro, a frequência do movimento é 1, e as duas massas se movem em fase, ambas se movendo para cima ou para baixo, juntas; a segunda massa se move duas vezes mais rápido do que a primeira. O segundo movimento tem frequência , e as massas se movem fora de fase uma em relação à outra, uma movendose para baixo enquanto a outra se move para cima, e vice-versa. Nesse modo, a primeira massa se move duas vezes mais rápido do que a segunda. Para outras condições iniciais que não são proporcionais à Eq. (iii) nem à Eq. (iv), o movimento das massas é uma combinação desses dois modos de vibração.