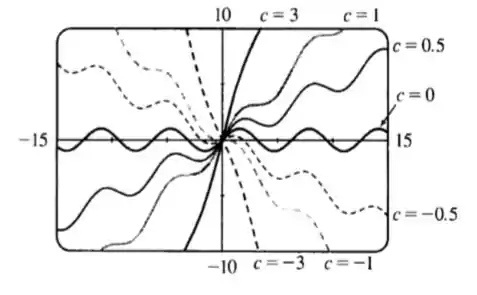
Descreva a mudança no gráfico de à medida que varia. Faça o gráfico de vários membros da família para ilustrar as tendências que você descobriu. Em particular, você deve investigar como os pontos de máximo e mínimo e os pontos de inflexão movem-se quando varia. Você deve também identificar qualquer valor intermediário de no qual o aspecto básico da curva mude.

, então não há ponto crítico quando . Se , então há infinitamente muitos pontos críticos. Se é a única solução de no intervalo , então os números críticos são , onde varia sobre os inteiros.

, então é côncava para baixo nos intervalos de forma . é côncava para cima nos intervalos de forma . Os pontos de inflexão de são os pontos , onde é um inteiro.

Se , então para todo , então é crescente e não tem valor extremo.

Se , então para todo , então é decrescente e não tem valor extremo.

Se , então está num intervalo de formato para algum inteiro . Esses são os intervalos em que é crescente. Similarmente, nós encontramos que é decrescente nos intervalos de forma . Assim, tem um máximo local nos pontos , onde tem os valores , e tem mínimo local nos pontos , onde nós temos . Os valores transitórios de são e . Os pontos de inflexão se movem verticalmente, mas não horizontalmente, quando muda.

Quando , não há valores extremos.

Para , os máximos são espaçados em pela horizontal, assim como os pontos mínimos.

O espaçamento horizontal entre máximos e mínimos adjacentes é regular e igual a quando , mas o espaço horizontal entre um máximo local e o mínimo mais próximo encolhe conforme se aproxima de .

Esboço do gráfico: