Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 6.3 - Ex. 1

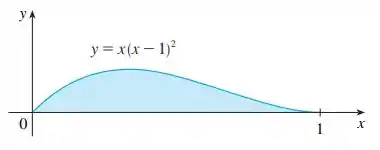
Considere S o sólido obtido pela rotação da região mostrada na figura em torno do eixo y . Explique por que é complicado usar fatias para encontrar o volume V de S . Esboce uma casca de aproximação típica. Quais são a circunferência e a altura? Use cascas para encontrar V .

Passo 1

Se nós decidirmos usar os métodos das fatias, nós teríamos primeiramente que localizar o ponto máximo local ( a , b ) de y = x ( x - 1 ) ² usando os métodos do Capítulo 4. Posteriormente, teríamos que resolver   y = x ( x - 1 ) ² para x em termos de y para obter as funções x = g 1 ( y ) e x = g 2 ( y ) mostrada a seguir

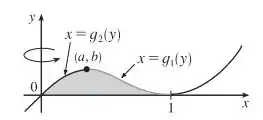
Esses passos seriam diferentes porque envolveriam a fórmula cúbica. Finalmente, nós teríamos que encontrar o volume usando

V = π ∫ 0 b { g 1 y 2 - g 2 y 2 } d y

Passo 2

Usando cascas, nós encontramos uma típica aproximação de cascas de raio x , logo, a circunferência é 2 π x , e a altura é y , que representa a função x ( x - 1 ) ² :

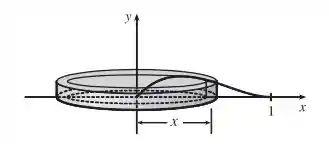
Passo 3

Com isso, temos que o volume total é

V = ∫ 0 1 2 π x x x - 1 2 d x = 2 π ∫ 0 1 ( x 4 - 2 x 3 + x 2 ) d x = 2 π x 5 5 - 2 x 4 4 + x 3 3 0 1 = π 15

Resposta

V = π 15 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se um fluido entra em um tanque semiesférico com raio de 3m , a uma taxa de 0,5m 3 / m i n , com que velocidade estará subindo quando a profundidade for de 1,5m ? [Sugestão Veja o exercicio 55 .]
A figura a seguir mostra as dimensões de uma pequena lâmpada em 10 pontos igualmente espaçados.(a) Use fórmulas de Geometria para fazer uma primeira estimativa do volume englobado pela parte de vidro
A figura abaixo mostra uma calota esférica de raio ρ e altura h cortada de uma esfera de raio r . Mostre que o volume V da calota pode ser expresso como: V = 1 3 π h 2 ( 3 r - h ) V = π h 6 3 e 2 + h
Encontre o volume da cunha descrita no Exercício 61 por fatiamento perpendicular ao eixo x .
Em 1635, Bonaventura Cavalieri, um aluno de Galileu, estabeleceu o seguinte resultado, chamado princípio de Cavalierri: Se dois sólidos tiverem a mesma altura, e se as áreas de suas seções transversai