Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 9.3 - Ex. 15
Nos problemas de 5 a 16:
a) Determine todos os pontos críticos do sistema de equações dado.
b) Encontre o sistema linear correspondente perto de cada ponto crítico.
c) Encontre os autovalores de cada sistema linear. O que você pode concluir sobre o sistema não-linear?
d) Desenhe um retado de fase do sistema não-linear para confirmar suas conclusões, ou para estendê-las nos casos em que o sistema linear não fornece informações definidas sobre o sistema não-linear.
15.
Passo 1
Os pontos críticos nos são dados pela solução das equações
Conseguimos ver naturalmente que x=0 e y=0 é um dos pontos críticos. Além disso temos, isolando y na primeira equação encontramos
Substituindo nasegunda equação encontramos
Plotando as funções notamos que somente tem raízes reais com valor aproximado de
Isso nos da que os pontos críticos são .
Passo 2
Note que e A matriz Jacobiana do campo vetorial é
Aplicando o ponto crítico temos
Os autovalores complexo .
Passo 3
No ponto a matriz do sistema linear é dado por
Os autovalores e . Os autovalores são reais de sinais opostos. Logo o ponto crítico do sistema linear associado é uma sela, que é instável. Resultado idêntico para
Passo 4
d)
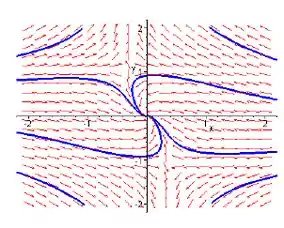
Observando conseguimos ver um expiral na origem.
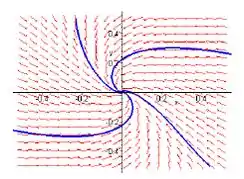
Próximo do ponto a natureza do ponto crítico é evidente.
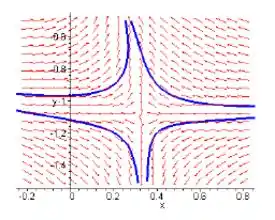
Baseado na tabela 9.3.1, os temos não lineares não afetam a estabilidade e tipo de cada ponto crítico.
Resposta
Ei, a resposta está no passo a passo :)