Um container para estocagem retangular com uma tampa aberta deve ter um volume de . O Comprimento da base é o dobro da largura. O material para a base custa $ por metro quadrado. O material para os lados custa $ por metro quadrado. Encontre o custo dos materiais para o mais barato desses contêineres.

Vamos começar desenhando nosso contêiner:

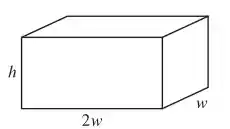
Com isso a gente já consegue ver que o volume do contêiner é:

Mas precisamos calcular a custo total do contêiner, que é a soma do custo da base com o da área lateral. Então, para a custo da área da base, teremos:

E para o custo da área lateral, temos:

Então, nosso custo total será dado pela soma de e , ou seja:

Da equação do volume no passo , podemos escrever:

Substituindo na equação do custo, ficamos com:

Tirando o MMC:

Agora vamos encontrar os pontos críticos da nossa equação. Primeiro, derivando , usando a regra do quociente, temos:

Agora igualando esse resultado a zero, vamos ter:

E isolando :

Então, substituindo esse resultado em , encontramos nossa altura:

Agora que temos as dimensões mínimas, só falta calcular o custo mínimo. Pra isso, vamos substituir os resultados que encontramos para e na equação do custo:

E calculando, temos:

Logo, o menor custo possível para esse contêiner será de $ .

Obs: Note que o valor pode resultar em algo ligeiramente diferente por conta de arredondamentos.

Valeu, galera! Até a próxima! 😉