Considere o seguinte problema: uma caixa sem tampa deve ser construída a partir de um pedaço quadrado de papelão, com metros de largura, cortando fora um quadrado de cada um dos quatro cantos e dobrando para cima os lados. Encontre o maior volume que essa caixa poderá ter.
- Faça vários diagramas para ilustrar a situação, algumas caixas baixas com bases grandes e outras altas com base pequena. Parece existir um volume máximo? Se a resposta for sim, estime-o.
- Faça um diagrama ilustrando a situação geral. Introduza a notação e marque no diagrama seus símbolos.
- Escreva uma expressão para o volume.
- Use a informação dada para escrever uma equação que relacione as variáveis.
- Use a parte (d) para escrever o volume como uma função de uma só variável.
- Acabe de resolver o problema e compare sua resposta com sua estimativa da parte (a).
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
Nessa aqui o enunciado nos deu um probleminha:
Uma caixa sem tampa deve ser construída a partir de um pedaço quadrado de papelão, com metros de largura, cortando fora um quadrado de cada um dos quatro cantos e dobrando para cima os lados. Então, devemos encontrar o maior volume que essa caixa poderá ter.
Pra isso, vamos seguir as instruções dos item (a) a (f) para construir alguns diagramas para ilustrar a situação, estimar um volume maáximo com base nesses diagrams, escrever uma expressão para o volume, escrever uma equação que relacione todas as variáveis e comparar o valor do volume máximo com a estimativa feita através dos diagramas.
Vamos lá!
Passo 2
a) Vamos começar esboçando os diagramas com as especificações da caixa que o enunciado nos deu. Há muitas formas de fazer isso, essas são algumas delas:
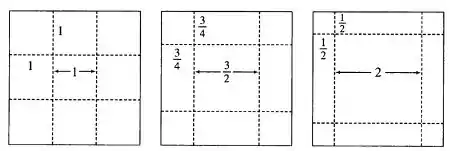
Temos que os volumes são, respectivamente e . Logo, parece que o volume máximo é .
Passo 3
(b) Agora vamos fazer um diagrama ilustrando a situação geral, definindo como o lado do quadrado a ser cortado e como o comprimento da base. Assim, temos:
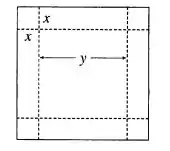
Passo 4
(c) Pra escrever uma expressão para o volume, vamos considerar o produto da área da base, , pela altura . Assim, teremos:
Passo 5
(d) Agora para relacionar todas as variáveis, vamos calcular o perímetro dessa caixa de papelão de comprimento . Dessa forma, podemos somar os comprimentos dos lados e obter:
E isolando , temos:
Passo 6
(e) Então, usando o resultado do passo anterior, vamos substituir essa expressão () na equação do volume, obtida no passo , e escrevê-lo em função de uma só variável. Assim, temos:
Passo 7
(f) Agora para comparar com a estimativa de volume máximo da parte (a), vamos encontrar os pontos críticos dessa equação do volume, derivando-a e igualando-a a zero.
Assim, derivando, temos:
E igualando esse resultado a zero:
Isolando , temos:
Ou
Como não podemos ter o valor , porque ela não tem uma altura nula, temos somente que:
Assim, obtemos:
Substituindo isso na expressão de , temos:
Logo, nosso volume máximo será dado por:
Que é o mesmo valor da estimativa na parte (a)
Valeu, galera! Até a próxima! 😉
Resposta
- O volume máximo é .
- O volume máximo é .