Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.7 - Ex. 17
Faça o exercício 16 supondo que o contêiner tenha uma tampa feita do mesmo material usado nos lados.
Passo 1
E aeee, belezinha? Bom... a questão nos pede para refazer a questão 16 só que supondo que o contêiner tenha uma tampa feita do mesmo material usado nos lados.
Em outras palavras, queremos calcular o custo dos materiais para que o contêiner saia o mais barato possível.
Isso tudo sabendo que o contêiner deve ter volume de e que o comprimento da base deve ser o dobro do comprimento da largura.
Também temos que o material dos lados custa por metro quadrado.
Dessa forma, vamos minimizar esses custos aplicando derivações.
Assim, lembre-se que para descobrirmos pontos de máximo ou mínimo, basta derivarmos uma função e igualar a zero!!
E aí? Bora lá aplicar?? 😉
Passo 2
Seja o contêiner:
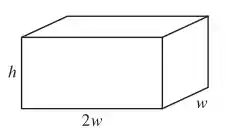
Temos que o volume do contêiner é:
Agora, precisamos calcular a custo total do contêiner, que é a soma do custo da base com o da área lateral com o da tampa.
Então começando pelo custo da base, temos:
Para a lateral, temos:
E, também:
Por fim, somando os valores calculados, temos o custo total:
Passo 3
Do volume, podemos escrever:
Substituindo no custo, ficamos com:
Para encontrar o mínimo, basta derivarmos e igualarmos a zero, então:
Igualando a zero:
Encontrando :
Passo 4
Agora, só falta calcular o custo mínimo :
Logo, o custo mínimo será de.
Obs: Note que o valor pode resultar em algo ligeiramente diferente por conta de arredondamentos.
Resposta
O custo mínimo será de .