Enunciado
Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 6.11 - Ex. 9
Se é continua em para todo x em [a,b], provar que:
Ilustrar graficamente, supondo
Passo 1
Vamos relembrar mais uma regra de integração.
Se são integráveis em [a,b] e para todo x pertencente a [a,b], então :
Passo 2
Vamos supor que
O enunciado nos deu que
Dessa forma podemos utilizar a propriedade vista acima de integral
Ou seja
Como queríamos demonstrar.
Passo 3
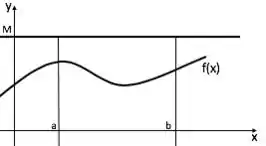
Agora vamos ilustrar graficamente o que ocorre, repare que a área abaixo do gráfico é menor do que a área para a reta y = M, o que implica nossa desigualdade demonstrada acima
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Use a Parte 2 do Teorema Fundamental do Cálculo para calcular a integral, ou explique por que ela não existe. ∫ - 5 5 2 x 3d x
Use a Parte 2 do Teorema Fundamental do Cálculo para calcular a integral, ou explique por que ela não existe. ∫ 0 π 6 c o s s e c θ c o t g θd θ
Use a Parte 2 do Teorema Fundamental do Cálculo para calcular a integral, ou explique por que ela não existe. ∫ 1 8 x 3d x
Use a Parte 2 do Teorema Fundamental do Cálculo para calcular a integral, ou explique por que ela não existe. ∫ π 2 π c o s s e c 2 ( θ )d θ
Use a Parte 2 do Teorema Fundamental do Cálculo para calcular a integral, ou explique por que ela não existe. ∫ 0 1 x 4 5d x