Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 5.3 - Ex. 34
Use a Parte 2 do Teorema Fundamental do Cálculo para calcular a integral, ou explique por que ela não existe.
Passo 1
Olá, meu amigo!
Temos essa integral:
E o exercício pede para resolve-lo, ou para explicar o porque não existe usando o TFC (Teorema Fundamental do Cálculo)
A segunda parte do teorema fundamental do cálculo, diz o seguinte:
Se for contínua em , então:
Onde é qualquer antiderivada de .
Imagina que estamos olhando para o gráfico de uma função, como uma montanha russa. Para dizer que essa função é integrável, precisamos saber se podemos medir a área sob essa curva, um detalhe a ser analisado é a continuidade:
Imagine que você está desenhando uma linha em um papel. Se essa linha é suave e contínua, sem levantar o lápis, é fácil medir a área abaixo dela. Mesmo que você tenha que levantar o lápis uma ou duas vezes, ainda dá para medir a área se essas interrupções não forem muitas ou não forem muito complicadas. Se você conseguir fazer isso, a função que desenhou é integrável.
Passo 2
Vamos pensar na nossa integral agora:
Podemos aplicar um pouco de trigonometria para trabalharmos com função mais comuns e mais fáceis para nós:
Então, vamos escrever da seguinte maneira:
Mas repare que quando integramos de até nós passamos pelo ponto . E aqui temos um problema, pois a função não está definida nesse ponto uma vez que o e o denominador seria .
Isso quer dizer que a integral não existe, pois a função é descontinua em .
Para ficar mais claro:
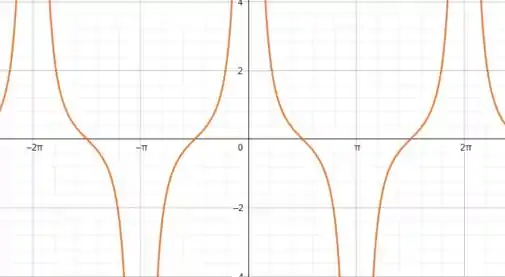
Repara que em e nos múltiplos de , ou seja, , sendo um numero inteiro, não temos uma definição. Logo se algum desses valores estiver dentro dos limites da integral, ele não existe!
Resposta
Não existe.