Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 5.3 - Ex. 27
Use a Parte 2 do Teorema Fundamental do Cálculo para calcular a integral, ou explique por que ela não existe.
Passo 1
Blzinha?
O exercício pede para explicar o porquê essa integral não existir:
O que torna uma função integrável?
Imagina que estamos olhando para o gráfico de uma função, como uma montanha russa. Para dizer que essa função é integrável, precisamos saber se podemos medir a área sob essa curva, um detalhe a ser analisado é a continuidade:
Uma função contínua, ou seja, sem buracos ou saltos, em um intervalo fechado é sempre integrável. Isso significa que, se você conseguir desenhar a função sem levantar o lápis do papel, ela é integrável nesse intervalo.
Funções Não Limitadas: Existem funções que não são limitadas e, portanto, não são integráveis. Um exemplo é a função , que não é limitada próximo a zero. Logo, não é integrável em intervalos que contenham zero no seu interior.
Resumindo:
Imagine que você está desenhando uma linha em um papel. Se essa linha é suave e contínua, sem levantar o lápis, é fácil medir a área abaixo dela. Mesmo que você tenha que levantar o lápis uma ou duas vezes, ainda dá para medir a área se essas interrupções não forem muitas ou não forem muito complicadas. Se você conseguir fazer isso, a função que desenhou é integrável.
Passo 2
A integral que ele nos pede para calcular é a seguinte:
Mas essa integral não existe, pois quando integramos de até passamos pelo ponto onde , mas a função é descontínua em uma vez que o denominador nunca pode ser . Portanto ela não será integrável.
Só para ficar mais claro, vamos ver o gráfico da função (não é um passo obrigatório!)
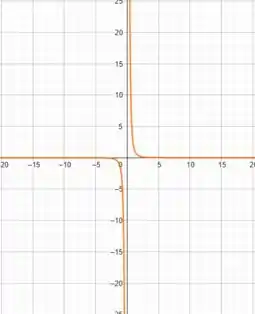
Note que em a função não é definida!
Entendeu tudinho? Responde aí!
Resposta
Não existe.