Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 9.4 - Ex. 14
Controle de uma população. O departamento de caça e pesca de determinado estado planeja emitir licenças de caça para controlar a população de cervos (um cervo por licença). Sabe-se que, se a população de cervos cair abaixo de certo nível , os cervos serão extintos. Sabe-se também que, se a população de cervos cresce acima da capacidade de carga , então a população decrescerá de volta a por doença e desnutrição.
- Discuta a razoabilidade do modelo a seguir em relação à taxa de crescimento da população de cervos em função do tempo:
- Explique por que esse modelo difere do modelo logístico Esse modelo é melhor ou pior do que o modelo logístico?
- Mostre que se para todo , então .
- O que acontece se para todo ?
- Discuta as soluções para a equação diferencial. Quais são os pontos de equilíbrio do modelo? Explique a dependência do valor de equilíbrio de em relação aos valores iniciais . Quantas licenças devem ser emitidas?
onde P é a população de cervos e r é uma constante positiva de proporcionalidade.
Inclua uma reta de fase.
Passo 1
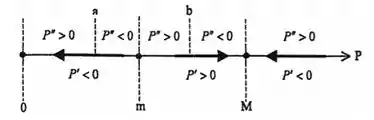
Para discutirmos a razoabilidade do modelo a seguir incluindo a reta de fase vamos ter que avaliar o seguinte: temos 3 pontos de equilíbrio (pontos onde ) que são e pela descrição dada no enunciado temos :
- Se ,então , quando o tempo tender ao infinito;
- Agora, se , então, a medida que o tempo cresce;
- Por fim, se , então, quando o tempo for tendendo para o infinito;
Assim, podemos construir a seguinte reta de fase
Passo 2
O modelo é diferente do modelo logístico pois se a população cair abaixo de isso vai nos levar a uma extinção da população. Esse modelo é provavelmente mais realista pois sabemos que algumas populações foram extintas quando sua população se tornou muito baixa.
Passo 3
Através da fórmula dada podemos observar que se teremos . Portanto, a curva está decrescendo. Agora, se observarmos quando temos uma solução da equação diferencial, como essa equação satisfaz as condições de existência e unicidade as trajetórias não podem se cruzar, então, quando .
Passo 4
A população tenderá a se extinguir como foi falado no enunciado.
Passo 5
Os pontos de equilíbrio para a equação diferencial dada são: e a quantidade de licenças a serem emitidas deve ser concedida de tal forma que se mantenha entre e , assim não corre risco de se extinguir e nem dos animais morrerem por fome e/ou desnutrição.
Resposta
Ei, a resposta está no passo a passo :)