Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 3.Revisão - Ex. 79
Um funil na forma de um cone tem de diâmetro do topo e de profundidade. A água está fluindo dentro do funil, a uma taxa de e para fora do funil, a uma taxa de . Com que velocidade o nível de água estará subindo quando a profundidade for de .
Passo 1
Trata-se de uma questão sobre taxas relacionadas. Note que a cada segundo, entram e saem de água do funil, de modo que a taxa de variação do volume de água dentro do funil é . O sinal de indica que o volume está aumentando, de modo que o nível de água está subindo.
Na figura a seguir representamos o funil quando a altura do nível de água for :
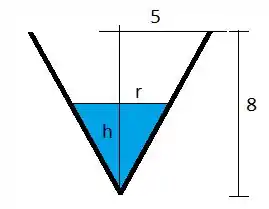
Nosso objetivo inicial é expressar o volume de água em função de para depois relacionar suas taxas de variação.
Passo 2
O volume de água é o volume de um cone de raio da base e altura :
Note que o volume depende tanto de como de : devemos eliminar uma dessas variáveis! Note que podemos usar semelhança de triângulos:
Assim,
Portanto,
Passo 3
Agora vamos relacionar as taxas de derivação aplicando a derivada em ambos os lados:
Queremos a velocidade com que o nível de água sobe (isto é, ) quando . Como , temos que
Assim,