Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.6 - Ex. 13
Esboce o gráfico à mão, usando as assíntotas e as intersecções com os eixos, mas não as derivadas. Então, use seu esboço como um roteiro na obtenção de gráficos (com uma ferramenta gráfica) que mostrem os aspectos mais importantes da curva. Use esses gráficos para estimar os valores máximo e mínimo.
Passo 1
Bom galera, nesse exercício queremos esboçar o gráfico da função apresentada
Usando apenas as assíntotas e as interseções com os eixos.
As interseções com os eixos são os pontos onde a função cruza o eixo , isso é:
E o ponto onde a função cruza o eixo , isso é:
Uma assíntota horizontal é um valor real para o qual a função tende quando tende para infinito:
Já uma assíntota vertical é um valor de no qual a função possui uma descontinuidade e tende para infinito.
Passo 2
Procurando pelas assíntotas.
Nossa função não é definida para e , pois assim teríamos uma divisão por zero.Logo, esses pontos são candidatos a assíntotas verticais.
Resolvendo os limites, temos
(Como o termo no denominador está elevado a uma potência par, ele tende a infinito positivo por ambos os lados.)
E
(Como o termo no denominador está elevado a uma potência ímpar, ele tende a infinito positivo pela direita e infinito negativo pela esquerda).
Dessa forma, em e em a função possui assíntotas verticais.
Para encontrar assíntotas horizontais vamos resolver o limite:
Como o termo no denominador possui maior potência, esse limite vai acabar tendendo para:
Dessa forma, nossa função é assintótica em relação a .
Podemos encontrar o ponto de intersecção igualando a zero
Dessa forma, intercepta o eixo em e em . Em não há interseção da curva com o eixo.
Passo 3
Procurando pelas interseções, vamos ver se ela cruza o eixo .
O que é verdade em
E
Dessa forma, intercepta o eixo em e em .
Agora procurando por uma interseção com o eixo .
Como dito anteriormente a função não é definida para , portanto, ela não cruza o eixo .
Passo 4
Esboçando o gráfico, temos
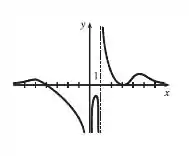
Resposta
Em e em a função possui assíntotas verticais. Nossa função possui assíntota horizontal em . Intercepta o eixo em e em . Em não há interseção da curva com o eixo.
