Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 3.Revisão - Ex. 80

Quando o último vagão de um trem passa por baixo de um viaduto, um automóvel cruza o viaduto numa rodovia perpendicular aos trilhos e 30   m acima deles. O trem está a 80   m / s , enquanto que o automóvel está a 40   m / s . Com que velocidade se afastam um do outro após 2   s ?

Passo 1

Trata-se de uma questão sobre taxas relacionadas. Se olharmos por cima, veremos que o trem se movimenta para a direita e o carro para cima no esquema abaixo:

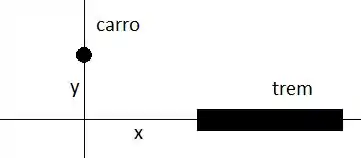
Para acharmos a velocidade com que eles se afastam, precisamos escrever uma função para a distância entre eles e em seguida derivar com relação ao tempo.

Passo 2

Como o carro passa sobre o trem à 30   m de altura, o plano que o carro se move está 30   m acima do plano que o trem se move (por isso enfatizei que na figura estamos com uma vista por cima). Sendo assim, a distância entre eles é dada por

d = 30 2 + x t 2 + y t 2

Todavia, note que como a velocidade do trem é 80   m / s , temos que x t = 80 t . Analogamente para o carro, obtemos y t = 40 t . Assim,

d = 900 + 80 t 2 + 40 t 2 = 900 + 6400 t 2 + 1600 t 2 = 900 + 8000 t 2

Portanto,

d = 10 9 + 80 t 2

Passo 3

Derivando d com relação ao tempo:

d ' = 10 ⋅ 1 2 9 + 80 t 2 ⋅ 160 t = 800 t 9 + 80 t 2

Agora fazendo t = 2 :

d ' = 800 ⋅ 2 9 + 80 ⋅ 4 = 16 00 329   m / s

Resposta

16 00 329   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dentre as infinitas retas tangentes à curva y = - sen ⁡ x que passam pela origem, existe uma que tem a maior inclinação. Use o método de Newton para encontrar a inclinação daquela reta com precisão de
Use o método de Newton para encontrar as coordenadas, com precisão de seis casas decimais, do ponto na parábola y = x - 1 2 que esteja mais próximo da origem.
Um pedaço de fio com 10m de comprimento é cortado em duas partes. Uma parte é dobrada no formato de um quadrado, ao passo que a outra é dobrada na forma de um triângulo equilátero. Como deve ser corta
Uma janela normanda tem a forma de um retângulo tendo em cima um semicírculo. (O diâmetro do semicírculo é igual à largura do retângulo). Se o perímetro da janela for 10m , encontre as dimensões da ja
As margens de cima e de baixo de um pôster têm 6c m , e as margens laterais medem 4c m . Se a área do material impresso sobre o pôster estiver fixa em 384c m ² ², encontre as dimensões do pôster com a