Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 3.Revisão - Ex. 81
Um homem com de altura caminha em direção a um edifício com uma velocidade de . Há um ponto de luz no chão a do edifício. Com que velocidade diminui a sombra do homem no edifício, quando ele está a do edifício?
Passo 1
Essa é uma questão bem clássica de taxa relacionada. O desenho a seguir representa um esquema da sombra do homem no prédio () quando a distância dele até o ponto de luz é .
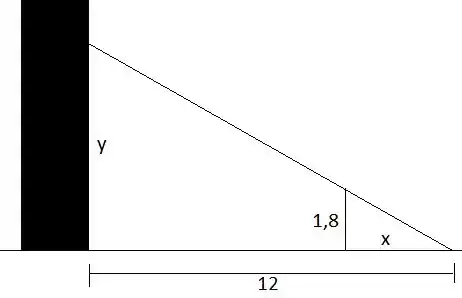
Como o homem se afasta do ponto de luz com velocidade , temos que . Agora precisamos achar uma relação entre e para tomarmos as derivadas.
Passo 2
Por semelhança de triângulo, temos que
Assim, derivando com relação ao tempo:
Passo 3
Quando a distância do homem ao prédio for , teremos . Como :
Assim, a velocidade com que a sombra diminui é .
Resposta
Exercícios de Livros Relacionados
Um varejista está vendendo 1200 tablets por semana a US $ 350 cada. O departamento de marketing estima que 80 tablets adicionais sejam vendidos a cada semana por cada US $ 10 que o preço for reduzido.
34. A função demanda para um certo produto é dada por p = - 2 x 2 + 9 sendo p o preço unitário em reais e x a quantidade demandada semanalmente. Determine o excedente de consumo se o preço de mercado
35. Um fornecedor de produtos estabelece que a quantidade de mercadoria a ser colocada no mercado está relacionada com o preço p , em reais, pela função p = x 2 + 5 x + 1 . Se o preço de mercado é igu
36. A quantidade demandada para um certo produto A está relacionado em reais, por p = 10 - 2 x e a quantidade x (em unidades) que o fornecedor está disposto a colocar no mercado está relacionada ao pr
37. Estima-se que um investimento gerará renda à taxa de R ( t ) igual a R $180.000 por ano pelos próximos três anos. Determine o valor presente deste investimento se a taxa de juros é de 6% ao ano co