Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 9.2 - Ex. 26a

Corrente em um circuito RL desligado Se o interruptor de um circuito RL for desligado depois de a corrente atingir o valor estacionário I = V / R , o decaimento da corrente ( esboçado graficamente aqui) obedece à equação:

L d i d t + R i = 0

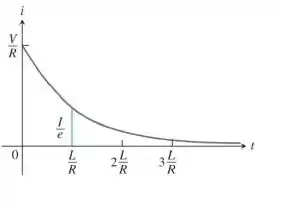
a-Resolva a equação para expressar i como uma função de t.

Passo 1

Temos aqui uma EDO, que é dada pela Lei de Kirchoff sem uma fonte externa:

L d i d t + R i = 0

Reescrevendo a equação Linear, temos que:

d i d t + R L i = 0

Para resolver essa questão temos que calcular primeiro o fator integrante v dado por:

v = e ∫ P ( t ) d t

e depois aplicar isso à seguinte expressão:

i t = 1 v t ∫ f ⋅ v t d t + c

Passo 2

Com as expressões acima podemos resolver a EDO. Vamos aqui nomear na nossa equação cada termo das expressões do passo 1.

P t = R L

f = 0

Passo 3

Calculando o fator integrante temos:

v = e ∫ R L d t = e R L t

Passo 4

Substituindo na solução da edo, temos que:

i t = 1 e R L t ∫ 0 ⋅ e R L t d t ⇒ i t = e - R L t A , onde A = c t e

i t = A e - R L t

Passo 5

A condição de contorno aqui é dada para a corrente estacionária, o qual é representada por i 0 = 0 :

i 0 = A e - R L 0 ⇒ i 0 = A e 0 = i 0

A = i 0

Resposta

Então a equação da corrente em função do tempo será:

i t = i 0 e - R L t

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma força eletromatriz (fem) de 200 volts é aplicada a um circuito R-C em série no qual a resistência é 1000 ohms e a capacitância, 5.10 - 6f a r a d . Encontre a carga q ( t ) no capacitor se i 0 = 0
Resolva a equação (6) supondo E t = E 0 . s e n ( ω t ) e i 0 = i 0
Em coordenadas polares, o momento angular de um corpo em movimento de massa m é definido por L = m r 2 d θ d t . Suponha que as coordenadas do corpo sejam r 1 , θ e r 2 ,θ nos intantes t = a e t = b ,
Suponha uma célula suspensa em uma solução contendo um solvente de concentração constante C s . Suponha ainda que a célula tenha volume constante C e que a área de sua superfície permeável também seja
A equação diferencial: d P d t = k . cos ⁡ t P Em que k é uma constante positiva, é frequentemente usada como um modelo de uma população sujeita à flutuações sazonais. Encontre P t e faça um gráfico d