Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 9.4 - Ex. 19

Corrente em um circuito RL. O diagrama a seguir representa um circuito elétrico cuja resistência total é uma constante R ohms e cuja autoindutância, mostrada como uma espiral, é L henries, também constante. Há um interruptor cujos terminais em a e b podem ser ligados para se conectarem a uma fonte elétrica de V   volts. Da Seção 9.2, temos

L ⋅ d i d t + R i = V ,

Onde i é a corrente em ampères e t é o tempo em segundos.

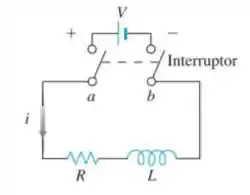
Use uma análise da reta de fase para esboçar a curva integral supondo que o interruptor no circuito R L tenha sido ligado no instante t = 0 . O que acontece com a corrente quando t → ∞ ? Esse valor é chamado de solução de estado estacionário.

Passo 1

Primeiramente, vamos isolar o termo d i d t na fórmula dada acima, assim

L ⋅ d i d t + R i = V →   L ⋅ d i d t = V - R i

d i d t = V L - R i L

Analisando a equação diferencial para quando d i d t = 0   vamos encontrar os pontos de equilíbrio, então, teremos

V L - R i L = 0

V L = R i L

V = R i

i = V R

Analisando a concavidade (segunda derivada) teremos

d 2 i d t 2 =   - R L ⋅ d i d t = - R L 2 ⋅ V R - i

Nossa reta de fase vai ser

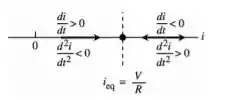
Passo 2

Se o botão for fechado em t = 0 , então i 0 = 0 e o gráfico da solução vai ser dado por

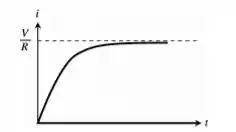
Ou seja, quando t → ∞ nosso estado estacionário vai ser dado por i e s t a d o   e s t a c i o n á r i o = V R .

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

16. A lei do resfriamento de Newton diz que a temperatura de um objeto varia a uma razãoproporcional à diferença entre sua temperatura e a temperatura ambiente. Suponha que atemperatura de uma xícara
14. Suponha que determinada população tem uma taxa de crescimento que varia com o tempo e queessa população satisfaz a equação diferencialdy/dt =(0,5 + sen t)y/5.(a) Se y(0) = 1, encontre (ou estime)
17. O calor transferido de um corpo para seu ambiente por radiação, baseado na lei de StefanBoltzmann,5 é descrito pela equação diferencial d u d t = - α u 4 - T 4 em que u(t) é a temperatura absoluta
15 . Suponha que determinada população satisfaz o problema de valor inicialdy/dt = r(t)y – k, y(0) = y0,em que a taxa de crescimento r(t) é dada por r(t) = (1 + sen t)/5, e k representa a taxa predató
18. Considere uma caixa isolada termicamente (um prédio, talvez) com temperatura interna u(t).De acordo com a lei do resfriamento de Newton, u satisfaz a equação diferencial d u d t =- ku - T ( t ) em