Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 1.3 - Ex. 71
Nos Exercícios 69-72, você explorara gráficamene a função seno geral
Enquanto altera os valores das constantes A, B, C e D. Utilize um CAS ou software de gráfico para seguir as instruções dos exercícios.
71. Deslocamento vertical D Defina as constantes , , .
a. Faça o gráfico de f(x) para os valores e no intervalo . Descreva o que acontece ao gráfico da função seno geral conforme os valores positivos de aumentam
b. O que acontece ao gráfico para valores negativos de ?
Passo 1
- Utilizando um software chegamos ao seguinte gráfico
- Utilizando:
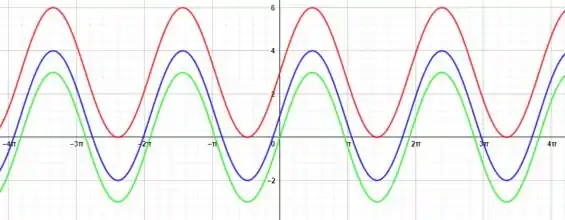
Verde (linha de baixo):
Azul (linha do meio):
Vermelho (linha de cima):
A medida que o valor de aumenta o gráfico é deslocado para cima unidades, ou seja se o valor de aumenta uma unidade o gráfico se move uma unidade para a cima.
Passo 2
Verde (linha do meio):
Vermelho (linha de cima):
Azul (pontilhado):
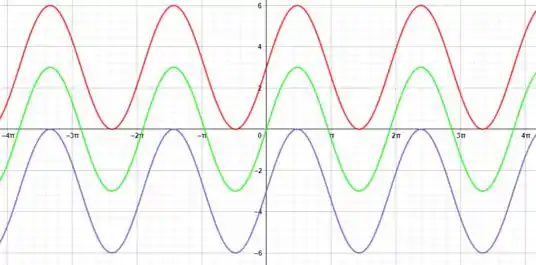
O gráfico tem um deslocamento de negativo do valor de . Se com positivo ele desloca o gráfico unidades para a cima, com negativo o gráfico é deslocado unidades para a baixo.
Resposta
Ei, a resposta está no passo a passo :)