Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 2.3 - Ex. 18b

18. Considere uma caixa isolada termicamente (um prédio, talvez) com temperatura interna u(t).De acordo com a lei do resfriamento de Newton, u satisfaz a equação diferencial

d u d t =   - k   u - T ( t )

em que T(t) é a temperatura do ambiente (externo). Suponha que T(t) varia como uma senoide;por exemplo, suponha que T(t) = T0 + T1 cos(ωt).(a) Resolva a Eq. (i) e expresse u(t) em termos de t, k, T0, T1 e ω. Observe que parte de suasolução tende a zero quando t fica muito grande; esta é chamada de parte transiente. O restanteda solução é chamado de estado estacionário; denote-a por S(t).(b) Suponha que t está medido em horas e que ω = π/12, correspondendo a um período de 24 horas para T(t). Além disso, sejam T0 = 60°F, T1 = 15°F e k = 0,2/h. Desenhe gráficos de S(t) e de T(t) em função de t nos mesmos eixos. A partir de seu gráfico, estime a amplitude R da parte oscilatória de S(t). Estime, também, a diferença de tempo τ entre os máximos correspondentes de T(t) e de S(t).(c) Sejam k, T0, T1 e ω não especificados. Escreva a parte oscilatória de S(t) na forma Rcos[ω(t – τ)]. Use identidades trigonométricas para encontrar expressões para R e τ. Suponhaque T1 e ω têm os valores dados no item (b) e desenhe gráficos de R e τ em função de k.

Passo 1

No item anterior descobrimos que nossa função solução é u t =   T 0 + k T 1 ω sin ⁡ ω t ω 2 + k 2 + k cos ⁡ ω t ω 2 + k 2 + C e - k t

T r ( t ) = C e - k t    

S t =   T 0 + k T 1 ω sin ⁡ ω t ω 2 + k 2 + k cos ⁡ ω t ω 2 + k 2  

Agora temos dados de contorno e queremos ver os gráficos relacionados com S t   ,   T ( t ) então nossa função S(t) fica

S t =   60 + 0,2 ⋅ 15 π 12 sin ⁡ π 12 t π 12 2 + 0,2 2 + 0,2 cos ⁡ π 12 t π 12 2 + 0,2 2  

E nossa função T(t) fica

T ( t )   =   T 0   +   T 1   c o s ( ω t ) .

T ( t )   =   60   +   15   c o s π 12 t

Passo 2

Assim os gráficos ficam da seguinte maneira

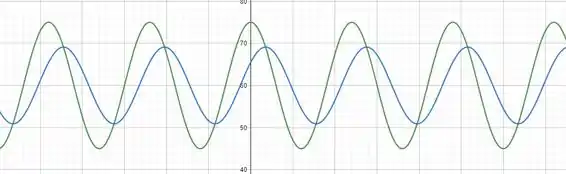
Onde a curva verde é T ( t ) e a curva em azul S ( t )

Passo 3

Precisamos analisar esse gráfico agora precisamos descobrir a amplitude de S(t) sendo

S t =   60 + 3 π 12 sin ⁡ π 12 t π 12 2 + 0,2 2 + 0,2 cos ⁡ π 12 t π 12 2 + 0,2 2  

A questão é como descobrir a amplitude de duas funções de onda ao mesmo tempo. Podemos usar da seguinte estratégia. A amplitude é a distancia da reta media ( a qual a função orbita ) até o máximo ou mínimo. Então podemos derivar S e descobrir qual ponto de t será essa posição. Então faremos

d S d t = 0

3 π 12 2 + 0 ,   2 2 π 2 144 cos ⁡ π t 12 - π 60 sin ⁡ π 12 t = 0

π 2 144 cos ⁡ π t 12 - π 60 sin ⁡ π 12 t = 0

sin ⁡ π 12 t cos ⁡ π 12 t = 60 π 144

π 12 t = arctan ⁡ 60 π 144

t = 12 ⋅ 0.9 + 12 n π  

Virou uma consta enorme né. MAS relaxa, decidi colocar o valor numérico de arco tangente por ser mais prático. E como só precisamos de um valor de t, podemos escolher n = 0 , dessa forma t fica

t = 12 ⋅ 0.9 π  

Aplicando isso em S(t) teremos a seguinte amplitude

A =   3 π 12 sin ⁡ π 12 ⋅ 12 ⋅ 0.9 π π 12 2 + 0,2 2 + 0,2 cos ⁡ π 12 ⋅ 12 ⋅ 0.9 π π 12 2 + 0,2 2

A =   3 π 12 sin ⁡ 0.9 + 0,2 cos ⁡ 0.9 π 12 2 + 0,2 2

Ficou um número bem esquisito, eu sei, mas se olharmos para o gráfico é a solução

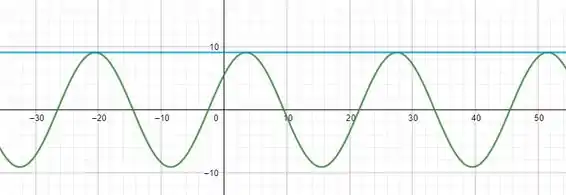
Onde a curva azul é o valor da amplitude (A) e a curva verde é S(t) que eu transladei para ela oscilar em torno do eixo x para ficar mais fácil a visualização.

Passo 4

Queremos, agora, saber a diferença de fazer entre T e S e para isso podemos fazer o seguinte truque.

T t + φ = S t

Onde φ é a fase que separa as duas ondas. Assim temos

15 c o s π 12 t + φ = 3 π 12 sin ⁡ π 12 t π 12 2 + 0,2 2 + 0,2 cos ⁡ π 12 t π 12 2 + 0,2 2  

Agora já que agora estamos na mesma fase, os máximos e mínimos estarão no mesmo ponto de t, logo se derivarmos e igualarmos a zero saberemos em que posições estarão nossos pontos críticos

d d t 15 c o s π 12 t + φ = 0

d d t 3 π 12 sin ⁡ π 12 t π 12 2 + 0,2 2 + 0,2 cos ⁡ π 12 t π 12 2 + 0,2 2 = 0

Por sorte nos já calculamos essa segunda integral

d d t 3 π 12 sin ⁡ π 12 t π 12 2 + 0,2 2 + 0,2 cos ⁡ π 12 t π 12 2 + 0,2 2 = 0 →   t = 12 ⋅ 0.9 π  

Assim podemos substituir esse valor na primeira integral e descobrir φ

d d t 15 c o s π 12 t + φ = 0

- 15 π 12 sin ⁡ π 12 t + φ = 0  

sin ⁡ π 12 t + φ = 0

sin ⁡ π 12 ⋅ 12 ⋅ 0.9 π + φ = 0

sin ⁡ 0.9 +   φ = 0

0.9 + φ = arcsin ⁡ 0

φ =   - 0.9

Se olharmos para o gráfico de T e S percebemos que acertamos ao descobrir a diferença de fase

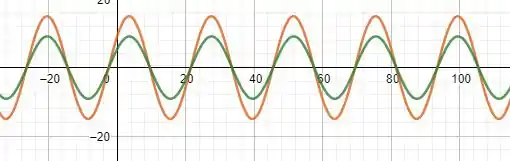
Terminamos por aqui. Te vejo na próxima resolução

: )

Resposta

A =   3 π 12 sin ⁡ 0.9 + 0,2 cos ⁡ 0.9 π 12 2 + 0,2 2

φ =   - 0.9

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Variação catastrófica no crescimento logístico. Suponha que uma população saudável de algumas espécies cresça em um ambiente limitado e que a população atual P 0 esteja bastante próxima da capacidade
Corrente em um circuito RL. O diagrama a seguir representa um circuito elétrico cuja resistência total é uma constante R ohms e cuja autoindutância, mostrada como uma espiral, é L henries, também cons
Controle de uma população. O departamento de caça e pesca de determinado estado planeja emitir licenças de caça para controlar a população de cervos (um cervo por licença). Sabe-se que, se a população
As equações diferenciais autônomas representam modelos de crescimento populacional. Use a análise da reta de fase para esboçar curvas integrais P ( t ) , selecionando diferentes valores iniciais P ( 0
Paraquedismo. Se um corpo de massa m que cai sob a ação da gravidade, desde o repouso, encontra uma força de resistência do ar proporcional ao quadrado da velocidade, então, a velocidade do corpo após