Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 3.5 - Ex. 65
Quociente da diferença centrada. O quociente da diferença centrada
É usado para aproximar no cálculo numérico porque (1) seu limite, quando , iguala-se a quando existe, e geralmente fornece melhor aproximação de , para dado valor de , do que o da diferença do quociente
Veja a figura a seguir.
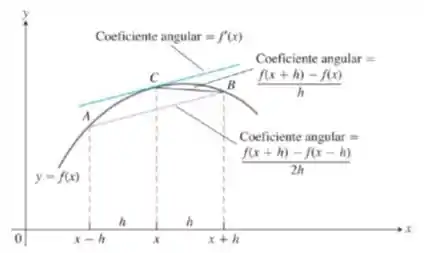
- Para ver com que rapidez o quociente da diferença centrada para converge para , esboce em um só gráfico e
- Para ver com que rapidez o quociente da diferença centrada para converge para , esboce em um só gráfico e
No intervalo para e . Compare esses resultados com aqueles obtidos no Exercício 63 para os mesmos valores de .
No intervalo para e . Compare esses resultados com aqueles obtidos no Exercício 64 para os mesmos valores de .
Passo 1
Precisamos começar esta questão com muita calma. Tem tanto texto que facilmente nos perdemos! Tanto a letra quanto a nos pede a mesma coisa, que é:
- Plotar 4 curvas diferentes;
- Comparar a convergência dos dados com os de uma questão anterior.
Portanto, iremos utilizar softwares para obter os gráficos das curvas e, posteriormente, iremos trazer os resultados da outra questão para poder comparar com os desta.
Passo 2
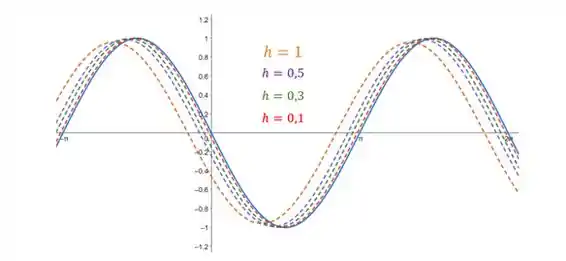
Vamos começar pelo esboço dos gráficos com diferentes valores de e da função cosseno. Desta forma, temos:
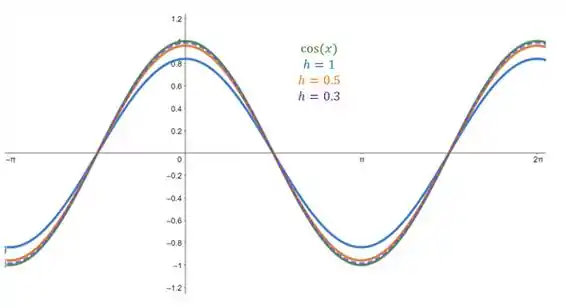
Como pode ser observado pelo gráfico, quando , o gráfico da função está muito próximo ao da função cosseno. Já quando , ele está basicamente sobreposto.
Passo 3
Vejamos o gráfico da questão 63:
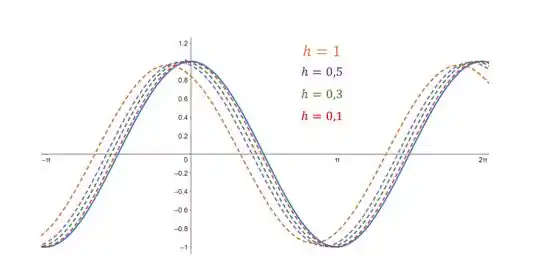
Como era esperado, a função da questão 63 demora mais a convergir. Basta observar a curva para poder comparar melhor com o gráfico que plotamos no Passo 2. Fica claro a diferença de aproximação a partir do momento que, para uma forma, a curva encontra-se quase que sobreposta, e para a outra, ainda está distante.
Observe que quando a curva ainda não está sobreposta.
Passo 4
Vamos repetir o procedimento para a letra agora. Plotando as curvas, temos:
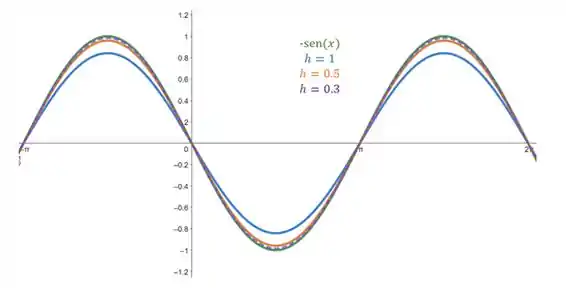
A mesma coisa que ocorreu na letra ocorre aqui. Quando a curva está muito próxima. Já quando , ela está basicamente sobreposta.
Passo 5
Vejamos agora o gráfico da questão 64.
Como era esperado, observe que somente quando é que a curva tende a se sobrepor. Novamente, verificamos que a aproximação de uma derivada por quociente de diferença centrada converge mais rapidamente!
Resposta
Ei, a resposta está no passo a passo :)