Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 3.7 - Ex. 45
Curva do diabo (Gabriel Cramer, 1750): Determine os coeficientes angulares para a curva do diabo nos quatro pontos indicados.
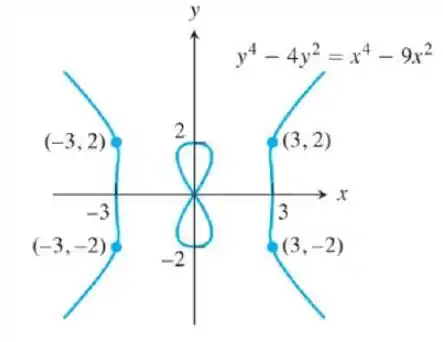
Passo 1
Questões de derivação implícita parecem ser difíceis, mas no final são tão simples quanto quaisquer outras questões de derivadas! Vamos destrinchar trecho por trecho desta questão.
Ela nos pede para determinar os coeficientes angulares em quatro pontos de coordenadas , por exemplo. Os coeficientes angulares nada mais são do que a derivada da função no ponto, isto é, o valor de neste ponto. Como derivaremos implicitamente, encontraremos funções do tipo:
Logo, basta substituir as coordenadas do ponto na função e assim obteremos o valor do coeficiente angular.
Sendo assim, vamos a nossa questão.
Passo 2
Vamos começar por derivar a nossa função implicitamente. Sendo assim, temos:
Passo 3
Agora, basta substituir as coordenadas dos nossos pontos. Para o ponto , temos:
Passo 4
Para o ponto , temos:
Passo 5
Já para o ponto de coordenadas , temos:
Passo 6
Para o ponto de coordenadas , temos:
Resposta
Os coeficientes angulares são:
- Ponto , ;
- Ponto , ;
- Ponto , ;
- Ponto , ;