Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 3.7 - Ex. 37
Nos Exercícios 31-40, verifique se o ponto dado faz parte da curva e determine as retas que são (a) tangentes e (b) normais à curva no ponto dado.
37.
Passo 1
Para verificar se o ponto faz parte da curva só precisamos substituir as coordenadas na função:
Portanto o ponto faz parte da curva.
Passo 2
a.
A reta tangente tem como inclinação o valor da derivada naquele ponto.
Derivando implicitamente a função:
O coeficiente angular da reta, tangente à função, no ponto , vale:
A reta tem sua equação da forma:
Passo 3
b.
A linha normal vai ter o mesmo ponto em comum.
Entretanto seu coeficiente angular irá ser oposto e inverso ao coeficiente angular da reta tangente, pois as retas são perpendiculares. Vamos mostrar o porquê disso.
Imagine duas retas e perpendiculares:
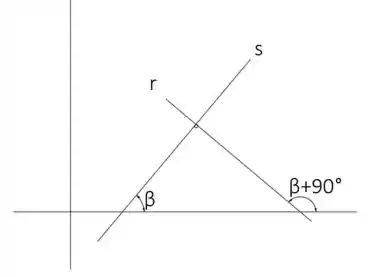
A e a são os coeficientes agulares das retas e , respectivamente.
Vamos calcular o valor de usando as fórmulas de adição estudada no Capitulo 1:
Ou seja:
Pronto, agora que a gente tem certeza que os coeficientes angulares das retas perpendiculares são opostos e inversos, vamos continuar calculando a equação da reta normal:
Resposta
O ponto faz parte da curva.
a.
b.