Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 5.6 - Ex. 50

Determine as áreas totais das regiões sombreadas

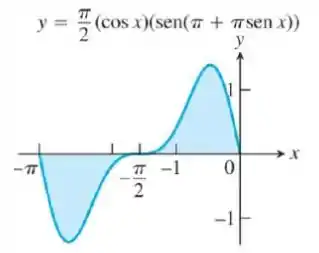
Passo 1

Precisamos determinar a área dada em azul na figura da questão. Desta forma, se f (x) >= g ( x ) ao longo de um intervalo [a , b] , então a área entre as curvas f ( x ) e g ( x ) é dada por:

A = int_a^b [f (x) - g (x)] d x

Desta forma, temos que identificar em cada caso quem é f ( x ) , g ( x ) e o intervalo [a , b] .

Passo 2

Vamos começar por montar qual a integral que devemos calcular. A área que devemos calcular é entre a função f (x) = (pi)/(2) cos x (sen (pi + pi sen x)) e g ( x ) = 0 . Além disto, observe a mudança do comportamento das funções. Entre [- pi , - pi // 2] , g (x) >= f ( x ) e entre o intervalo [- pi // 2 , 0] ocorre o contrário. Desta forma, a área da região em azul é dada por:

A = int_(- pi)^(- pi // 2) - (pi)/(2) cos x (sen (pi + pi sen x)) d x + int_(- pi // 2)^0 (pi)/(2) cos x (sen (pi + pi sen x)) d x

Observe que é necessário separar em uma soma de integrais devido à mudança no comportamento da imagem das funções.

Passo 3

Vamos agora aplicar uma propriedade bastante importante que facilitará e muito na resolução do nosso problema (e quem não quer facilidade!). Vocês conseguem observar a simetria da nossa função f ( x ) em torno da reta x = - pi // 2 ? Por causa desta simetria, temos a seguinte relação:

int_(- pi)^(- (pi)/(2)) - (pi)/(2) cos x (sen (pi + pi sen x)) d x = int_(- (pi)/(2))^0 (pi)/(2) cos x (sen (pi + pi sen x)) d x

Portanto, podemos escrever a nossa área através de apenas uma integral! Então, temos:

A = 2 int_(- pi // 2)^0 (pi)/(2) cos x (sen (pi + pi sen x)) d x

Passo 4

Agora, enfim, precisamos resolver a nossa integral. Vamos fazer a mudança u = pi + pi sen x . Consequentemente, d u = pi cos x d x . Além disto, vamos modificar os limites de integração. Portanto, quando x = 0 ⟹ u = pi , já quando x = - pi // 2 ⟹ u = 0 . Fazendo esta mudança, temos:

A = 2 int_(- pi // 2)^0 (pi)/(2) cos x (sen (pi + pi sen x)) d x = int_0^(pi) sen u d u

A = int_0^(pi) sen u d u = ([- cos u]|_0^(pi)

A = - cos pi - (- cos 0)

A = 1 + 1 = 2

Resposta

A = 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o centro de massa da região A dada por 4 x 2 + y 2 ≤ 4 , y ≥ 0 . (Sugestão: Para o cálculo de x c aproveite a simetria da figura.)
Seja A o conjunto do plano de todos os ( x , y ) tais que 0 ≤ a ≤ x ≤ b , 0 ≤ f x ≤ y ≤ g ( x ) , onde f e g são supostas contínuas em [ a , b ] . Image A como uma lâmina delgada, homogênea, de modo q
Esboce a região delimitada pelas curvas indicadas e encontre sua área. y = 12 - x 2 , y = x 2 - 6
Esboce a região delimitada pelas curvas indicadas e encontre sua área. x = 2 y 2 , x = 4 + y 2
Esboce a região delimitada pelas curvas indicadas e encontre sua área. y = e x , y = x e x ,x = 0