Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.5 - Ex. 42

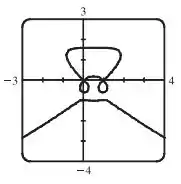
  1. A curva com equação

    2. 2 y 3 + y 2 - y 5 = x 4 - 2 x 3 + x 2

    tem sido comparada com um “vagão sacolejante”. Use um SCA para fazer essa curva e descubra o porquê desse nome.

  2. Em quantos pontos essa curva tem retas tangentes horizontais? Encontre as coordenadas x desses pontos.

Passo 1

Nessa questão devemos usar um SCA (uma calculadora gráfica) para descobrir por que a curva

2 y 3 + y 2 - y 5 = x 4 - 2 x 3 + x 2

Tem o nome de vagão sacolejante.

Por fim, vamos encontrar os valores de x onde a curva possui reta tangente horizontal.

Para isso, vamos deriva-la implicitamente e igualar a derivada a zero

(para derivar implicitamente basta derivar ambos os lados da equação e quando for derivar em y multiplicar por y ' ).

Passo 2

Usando uma calculadora gráfica, você obtêm o gráfico a seguir, que realmente parece com o tal vagão:

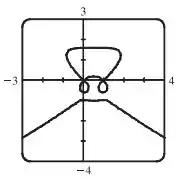
Passo 3

Para achar as retas tangentes, a gente deriva implicitamente a equação:

d d x 2 y 3 + y 2 - y 5 = d d x x 4 - 2 x 3 + x 2

6 y 2 y ' + 2 y   y ' - 5 y 4 y ' = 4 x 3 - 6 x 2 + 2 x

E por fim, colocamos o y ' em evidência, obtendo:

y ' = 4 x 3 - 6 x 2 + 2 x 6 y 2 + 2 y - 5 y 4

Queremos que essa derivada seja igual a zero

4 x 3 - 6 x 2 + 2 x 6 y 2 + 2 y - 5 y 4 = 0

Para que isso seja verdade, é necessário que:

4 x 3 - 6 x 2 + 2 x = 0

Colocando o x em evidência, obtemos:

x 4 x 2 - 6 x + 2 = 0

Logo,

x 0 = 0

ou

4 x 2 - 6 x + 2 = 0

Resolvendo essa equação de segundo grau você irá obter:

x 1 = 1 2

x 2 = 1

Esses são os pontos onde há uma reta tangente horizontal.

Resposta

x 0 = 0

x 1 = 1 2

x 2 = 1

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use a derivação implícita para encontrar a equação da reta tangente à curva no ponto dado. x 2 + 2 x y - y 2 + x = 2 , ( 1,2 ) (hipérbole)
Mostre, fazendo a derivação implícita, que a tangente à elipse x 2 a 2 + y 2 b 2 = 1 No ponto ( x 0 ,   y 0 ) é x 0 x a 2 + y 0 y b 2 = 1
Mostre que a soma das coordenadas das intersecções com os eixos x e y de qualquer reta tangente à curva x + y = c é igual a c .
Encontre uma equação da reta tangente à hipérbole x 2 a 2 - y 2 b 2 = 1 No ponto ( x 0 ,y 0 ) .
Mostre, usando a derivação implícita, que qualquer reta tangente, em um ponto P , a um círculo com centro O é perpendicular ao raio O P .