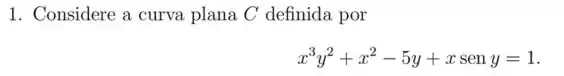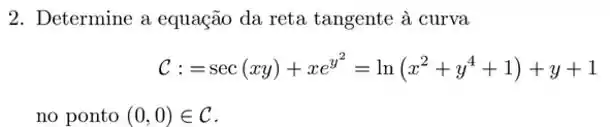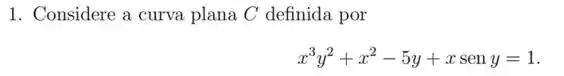Exercícios de Reta Tangente – Derivadas Implícitas - Lista de Exercícios Resolvida
Questão 2
Encontre pontos na curva onde a tangente é paralela (a) ao eixo e (b) ao eixo .
Ver solução completaQuestão 3
Seja a reta tangente à curva dada pela equação
No ponto . Calcule a área do triângulo formado por e os eixos coordenados.
Veja abaixo uma figura ilustrativa:
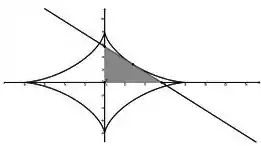
Questão 4
Considere a curva definida pela equação . Calcule e encontre a aproximação linear à curva no ponto .
Ver solução completaQuestão 5
Considere a curva definida pela equação . Calcule e encontre a aproximação linear à curva no ponto .
Ver solução completaQuestão 6
Considere a curva definida pela equação .
- Calcule .
- Encontre a equação da reta tangente a curva no ponto .
Questão 7
Seja uma função derivável num intervalo aberto que contém e tal que
Para todo . A equação da reta tangente ao gráfico de no ponto é:
Questão 9
Considere a curva da figura ao lado conhecida como cissóide de Diócles cuja equação é .
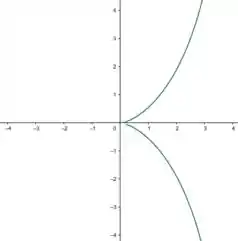
b) Obtenha as equações das retas tangentes ao gráfico da curva nos pontos em que .
Ver solução completaQuestão 11
Considere a curva plana definida por:
Seja a derivada de implicitamente definida como função de .
- Encontre uma expressão para em termos de e .
- Obtenha uma equação para a reta tangente à curva no ponto de coordenadas .
Questão 12
Considere a curva plana dada pela equação
Determine equações da reta tangente e da reta normal a esta curva no ponto .
Ver solução completaQuestão 13
Seja um ponto da curva tal que a reta tangente em faz um ângulo de com o eixo . Quais são as coordenadas de ?
Ver solução completaQuestão 14
Considere a curva definida pela equação . Calcule e encontre a equação da reta tangente a curva no ponto .
Ver solução completaQuestão 15
Dizemos que duas curvas são tangentes em um determinado ponto quando possuem a mesma reta tangente neste ponto. Mostre que a parábola é tangente à cúbica no ponto .
Ver solução completaQuestão 16
Considere a curva definida pela equação . Encontre a equação da reta tangente à curva no ponto .
Ver solução completaQuestão 18
Seja uma função derivável dada implicitamente pela equação
A reta tangente ao gráfico de no ponto é paralela à reta de equação:
Questão 19
Seja uma função derivável dada implicitamente pela equação
A reta tangente ao gráfico de no ponto é paralela à reta de equação:
Questão 20
Mostre que o ponto está na curva e determine as equações da reta tangente e da reta normal à curva nesse ponto.
Ver solução completaQuestão 23
Considere a curva da figura ao lado conhecida como cissóide de Diócles cuja equação é .
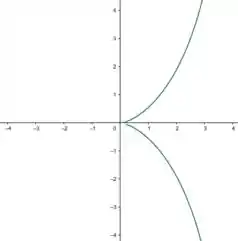
- Obtenha a equação da reta tangente ao gráfico da curva em ;
Questão 25
Seja uma função inversível e diferenciável tal que e . Então a equação da reta tangente ao gráfico da função inversa em é:
Ver solução completaQuestão 26
Considere a curva C dada por :
- Determine uma expressão para em termos de e .
- Encontre a equação da reta tangente à curva C no ponto (1,1).
Questão 27
Considere a leminiscata de equação (figura ao lado). Determine os quatro pontos da leminiscata em que as retas tangentes são horizontais. Ache, em seguida, os dois pontos em que as tangentes são verticais.
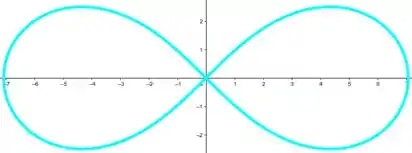
Questão 29
Considere a curva dada por .
a) Determine em termos de e .
b) Encontre a equação da reta tangente a curva no ponto
Ver solução completaQuestão 30
4. Determine uma reta que seja paralela à reta e que seja tangente à curva .
Ver solução completaQuestão 31
6. Sabeno que o ponto pertence à curva e que a equação da reta tangente à curva nesse ponto é dada por , determine e .
Ver solução completaQuestão 34
Considere a curva definida pela equação .
(b) Encontre a equação da reta tangente à curva no ponto .
Ver solução completaQuestão 35
A função é conhecida como fólio de Descartes. Encontre a equação da reta tangente à função no ponto .
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 36
Seja uma constante positiva. Mostre que a soma das coordenas das interseções com o eixo X e Y de qualquer reta tangente a curva:
É constante e igual a .
Ver solução completaQuestão 37
Encontre a equação da reta tangente à curva cissóide de Diocles
No ponto .
Ver solução completaQuestão 39
(9) Se são diferenciáveis em , então e são necessariamente diferenciáveis em ? Se e são diferenciáveis em , quais as condições sobre garantem que seja diferenciável em ?
Ver solução completaQuestão 40
2. Determine todos os pontos sobre a curva definida pela equação para os quais a reta tangente à curva no ponto é paralela à reta de equação .
Ver solução completaQuestão 41
Considere a curva definida pela equação . Calcule e encontre a equação da reta tangente a curva no ponto ().
Ver solução completaQuestão 43
Determine os pontos da curva
Com coordenada , onde a reta tangente é paralela ao eixo
Ver solução completaQuestão 44
Mostre que o ponto está na curva e determine as equações da reta tangente e da reta normal à curva nesse ponto.
Ver solução completaQuestão 45
Encontre a equação da reta tangente `a curva de equação no ponto (1, −1).
Ver solução completa