Enunciado
Cálculo - Dennis G. Zill - Equações Diferenciais - Vol 1- Ed: 3º - Capítulo 1.2 - Ex. 15
Uma curva C no plano reflete os raios de luz de tal modo que todo raio L paralelo ao eixo y é refletido para um único ponto 0. Determine a equação diferencial para a função que descreve a forma da curva C. (O fato de o ângulo de incidência ser igual ao ângulo de reflexão é um princípio da ótica.) [Sugestão: a Figura 1.22 mostra que a inclinação da reta tangente em é e podemos escrever . (Por quê?). Não tenha receio de usar as identidades trigonométricas.]
Passo 1
Nesse problema, temos o seguinte esquema
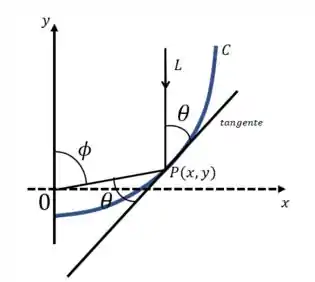
Vamos entender o que acontece: quando um raio de sol () é paralelo ao eixo e bate na curva , o seu reflexo bate na origem, sacou?
E a gente quer a equação diferencial para , que é a equação da curva .
Passo 2
Vamos começar comprovando a informação do enunciado de que . Para isso, vamos levar a reta de até o eixo :
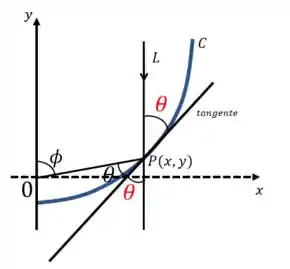
Os ângulos em vermelho são iguais, pois são opostos pelo vértice.
E aí, vamos ignorar a reta tangente rapidinho e imaginar esses dois triângulos:
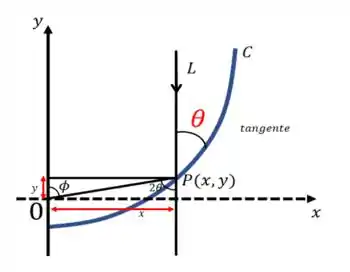
Por semelhança de triângulos, temos que
E por trigonometria, temos ainda que
Passo 3
Outra informação que temos é que a inclinação da reta tangente à curva no ponto é .
O que a inclinação da reta tangente representa mesmo???.......
Issooo, a derivada!! Então olha só mais um dado pro exercício:
Usando que :
Mais duas identidades trigonométricas que vamos usar: e :
Então:
E
Passo 4
Então vamos lá utilizar as informações que conseguimos até agora
Temos
Por identidade trigonométrica, temos que :
Mas vimos no passo anterior que :
Multiplicando em cruz:
E, por fim, reformulando:
