Enunciado
Cálculo - Dennis G. Zill - Equações Diferenciais - Vol 1- Ed: 3º - Capítulo 1.2 - Ex. 20
Suponha uma abertura passando pelo centro da terra. Um corpo de massa é atirado na abertura. Denote por a distância do centro da terra à massa no instante . Veja a figura 1.25.
a) Sejam a massa da terra e a massa da porção da terra limitada por uma esfera de raio . A força da gravidade atuando em é , em que o sinal de subtração indica que a força é uma atração. Use este fato para mostrar que
Sugestão: Suponha que a terra seja homogênea, isto é, a densidade é constante. Use .
b) Use a segunda lei de Newton e o resultado da parte (a) para deduzir a equação diferencial
Em que .
Passo 1
Olha que loucura o que ta acontecendo aqui, a gente meio que abre um buraco que atravessa a Terra e joga um objeto de massa lá dentro........???
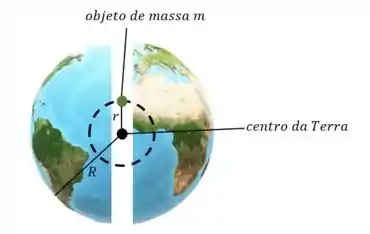
Beleza beleza, vamos aceitar e entender cada um dos itens
a) - Temos que a massa da Terra vale
- é a distância do objeto ao centro da Terra
- A massa da partezinha da Terra que ta na esfera de raio é
E aí temos que a força gravitacional em vale
Agora o nosso objetivo é provar que
Bora lá!
Passo 2
Vamos usar a sugestão do enunciado utilizando a fórmula
Lembrando que o volume de uma esfera de raio é , temos que a massa da Terra é
E também temos a massa :
De , temos:
Substituindo em :
Agora vamos substituir em :
Cortando os termos em comum:
Que é exatamente a expressão !! Então realmente, a expressão pode ser escrita como a expressão , e pra isso só utilizamos a fórmula de densidade em e , iháááá :P
Passo 3
b) Nesse item, precisamos deduzir essa equação diferencial:
Em que .
Usando a segunda lei de Newton, temos
Mas a aceleração é a segunda derivada da posição, então:
Também temos a força gravitacional (aquela que comprovamos no item anterior) agindo sobre o corpo, então:
Mas temos , então, substituindo:
E, por fim:
É issooo, ta provado hihi