Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 2.3 - Ex. 14-a

14. Suponha que determinada população tem uma taxa de crescimento que varia com o tempo e queessa população satisfaz a equação diferencial

dy/dt =(0,5 + sen t)y/5.

(a) Se y(0) = 1, encontre (ou estime) o instante τ no qual a população dobrou. Escolha outrascondições iniciais e determine se o tempo de duplicação τ depende da população inicial.(b) Suponha que a taxa de crescimento é substituída pelo seu valor médio 1/10. Determine otempo de duplicação τ nesse caso.(c) Suponha que o termo sen t na equação diferencial é substituído por sen(2πt); ou seja, avariação na taxa de crescimento tem uma frequência substancialmente mais alta. Qual o efeitodisto no tempo de duplicação τ?(d) Faça o gráfico das soluções obtidas nos itens (a), (b) e (c) em um único conjunto de eixos.

Passo 1

Então temos a equação

dy/dt =(0,5 + sen t)y/5.

E queremos saber quando o nosso y dobra de valor. Bem pra começar temos uma boa notícia, essa é uma equação separável (ou seja, podemos jogar tudo que é y para um lado e tudo o que é t para o outro) . Uma das mais tranquilas de se resolver olhando de forma geral dentre as equações diferenciais. Entao beleza! Vamos cair \o/

Passo 2

d y d t = ( 0,5   +   s e n   t ) y / 5 .

1 y d y   = 0,5   +   s e n   t 5   d t

Vamos integra rem ambos os lados

ln ⁡ y   = t 10 - cos ⁡ t 5 + C

y = e t 10 - cos ⁡ t 5 + C

Podemos manipular a constante arbitraria, de forma que ela fique assim

y = C e t 10 - cos ⁡ t 5

Show! Conseguimos descobrir nossa equação !!!

Passo 3

Agora so nos resta usar os dados de contorno para encontrarmos C

y(0) = 1

Com isso nossa equação fica

y = C e t 10 - cos ⁡ t 5

1 = C e - 1 5

C = e 1 5

Com isso nossa equação se conclui como

y = e 1 5 ⋅ e t 10 - cos ⁡ t 5

y = e t 10 - cos ⁡ t 5 + 1 5

Passo 4

Agora como queremos que nossa população dobre entoa nossa função vai ser

y   t = 2

2 = e t 10 - cos ⁡ t 5 + 1 5

ln ⁡ 2 = t - 2 cos ⁡ t + 2 10

10 ln ⁡ 2 - 2 = t - 2 cos ⁡ t  

Não existe solução analítica dessa função, mas podemos fazer uma solução geométrica. Cruzar as curvas 10 ln ⁡ 2 - 2 e t - 2 cos ⁡ t e ver os pontos de interseção

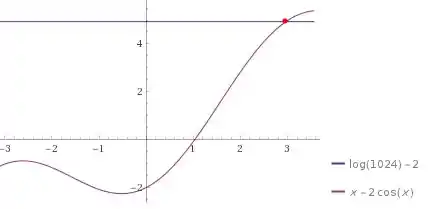
Logo nosso t = 2,96   . O enunciado pergunta se o tempo para dobrar continua o mesmo para qualquer valor inicial. E a resposta é sim pois se

y 0 = y 0

y t = 2 y 0

Nossa equação continua com o mesmo formato

2 = e t 10 - cos ⁡ t 5 + 1 5

Terminamos por aqui. Te vejo na próxima resolução

: )

Resposta

t = 2,96

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Suponha que a bola do exercício 58 caia de cima da casa.a)Quanto tempo irá decorrer até ela atingir o solo?(Dados do exercício 58: A altura inicial da bola em relação ao solo é de 19m.)
Uma partícula move-se em linha reta, s cm é a distância orientada dapartícula à origem em t s, v cm/s é a velocidade da partícula em t s e a cm/s² é a sua aceleração em t s. Sabendo que a = 3 t + 4 e
Uma partícula move-se em linha reta, s cm é a distância orientada dapartícula à origem em t s, v cm/s é a velocidade da partícula em t s e a cm/s² é a sua aceleração em t s. Sabendo que a = 6 cos ⁡ 2
Um fabricante de brinquedos tem um novo brinquedo para lançar no mercado e deseja determinar o preço de venda do brinquedo, tal que o lucro total seja máximo. Pela análise do preço e da demanda de out
Ache uma equação da curva que passe pelo ponto 1 6 π ,0 e para qual a inclinação de qualquer ponto ( x , y ) sobre ela seja ( 2 y + 4 ) / tg ⁡ x .