Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 1.1 - Ex. 72
Custos industriais. Uma usina elétrica está localizada em um trecho de rio que tem pés de largura. Os custos para passar um novo cabo da usina até uma localização na cidade 2 milhas rio abaixo, do lado oposto do rio, são de $180 por pé de cabo cruzando o rio e $100 por pé de cabo estendido por terra.
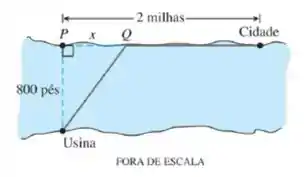
- Suponha que o cabo saia da usina em direção ao ponto do lado oposto, que fica pés distantes do ponto na margem oposta à usina. Escreva uma função que forneça o custo para passar o cabo em função da distância .
- Gere uma tabela de valores para determinar se a localização de menor custo para o ponto é menor ou maior que pés a partir do ponto .
Passo 1
Primeiramente, precisamos obter uma função para expressar o custo total para passar o cabo da usina até a cidade. Para isto, vamos separar o comprimento do cabo em duas partes. Seja a distância da usina até o ponto , passando sobre o rio, e a distância do ponto até a cidade, passando pela terra. Desta forma, o custo total é:
Agora, nos falta descobrir quais são as funções e . Para isto, utilizaremos a geometria do problema, conforme pode ser visto pela imagem da questão.
Após descobrirmos a função custo, para resolvermos a letra , precisamos montar uma tabela e analisar o comportamento do custo. Isto é, se depois de 2000 pés a função é crescente ou se decresce.
Desta forma, vamos as contas.
Passo 2
Vamos começar por determinar quem é a função . Pelo desenho, podemos inferir um triângulo retângulo, em que os catetos são pés e e a nossa hipotenusa é . Desta forma, utilizando o teorema de Pitágoras, temos:
Passo 3
Agora, precisamos expressar quem é . Como a distância do ponto até a cidade é igual a 2 milhas, que é igual a 10560 pés, temos então:
Passo 4
Agora que obtemos as funções e , vamos substituir seus valores na função escrita no Passo 1, e assim, obteremos a função custo em função do comprimento . Portanto, temos:
Passo 5
Agora, podemos montar a nossa tabela para analisar o que acontece com a nossa função. Vejamos abaixo a tabela:
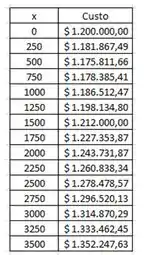
Conforme podemos observar pela tabela. À medida que aumenta até 500 pés, o valor do custo diminui. Depois deste valor, ele começa a crescer. Portanto, podemos esperar que o valor de menor custo é o valor de menor que 2000 pés.
Resposta
- A função custo é:
- O valor de que ocasiona em um menor custo é menor que 2000 pés.