Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 1.1 - Ex. 71
É preciso construir um cercado na forma de um triângulo retângulo isósceles com pernas de pés de comprimento e hipotenusa de pés de comprimento. Se o revestimento custa $5 pés para as penas e $10 pés para a hipotenusa, represente o custo total da manufatura em função de .
Passo 1
A questão nos pede para determinar o custo de manufatura. Ele é obtido através do produto do comprimento de cercado pelo preço de cada material. Desta forma, temos:
A função acima já descreve o custo do cercado. Entretanto, ela é uma função de duas variáveis: as pernas do cercado e a hipotenusa . Precisamos obter uma função de apenas 1 variável . Desta forma, precisamos encontrar alguma forma de escrever .
Desta forma, vamos as contas.
Passo 2
O cercado possui uma forma de triângulo retângulo isósceles, como pode ser observado abaixo:
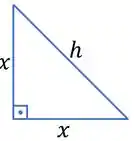
Os catetos são iguais pois é um triângulo isósceles. Como ele possui um ângulo reto, podemos aplicar o teorema de Pitágoras. Assim temos:
Passo 3
Se substituirmos o na função escrita no Passo 1, temos:
Logo, conseguimos escrever o custo de manufatura como função de .