Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 1.1 - Ex. 7
Determine se a curva é um gráfico de uma função . Se o for, determine o domínio e a imagem da função.
Passo 1
Eaee, belezinha??
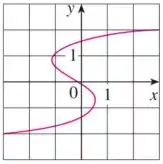
Bom... a questão nos dá a seguinte curva:
Queremos saber se a curva é um gráfico de uma função de .
Para isso, devemos verificar se a função associa apenas um valor para cada . Como assim associa?
Pra ser uma função de , então pra cada , a gente vai ter apenas 1 único valor de
Ué mas as vezes a gente tem 2 pontos com o mesmo . É verdade, e nesse caso ainda é uma função de , mas ao contrário não pode!
Uma forma de verificar isso é através do teste da reta vertical que vamos aplicar aqui mais pra frente.
E se for uma função, então temos que encontrar o domínio e a imagem. Domínio é o conjunto de valores de entrada () e imagem o conjunto de valores de saída () que a função possui.
E aí?? Bora lá?? 😉
Passo 2
Bom... vamos lembrar que uma função associa apenas um valor para cada .
Ou seja, se um gráfico estiver associando mais de um valor no eixo para um único valor , o mesmo não pode ser gráfico de uma função de .
Verificamos isso com um teste fácil.
Se pudermos traçar uma reta vertical que passe por mais de um ponto do gráfico, então ele não é uma função.
Esse é o teste da reta vertical (matemáticos e suas nomenclaturas sempre criativas).
Veja só! 😬
Passo 3
Traçando uma reta vertical que passe por , temos que essa reta passará por pontos do gráfico, veja:
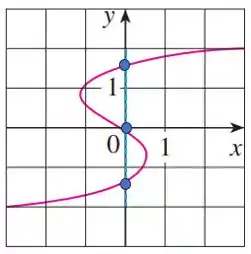
Logo, não é gráfico de uma função.
E aí! entendeu tudo? Responde Aí! 😁
Resposta
Não é uma função