Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 3.2 - Ex. 25b
25. Dada . (a) Prove que não existem. (b) Prove que . (c) Faça um esboço do gráfico de
Letra ( b )
Passo 1
O que ele nos pede nesta opção é para determinarmos qual é o limite da função derivada à esquerda e à direita. Além disso, sabemos que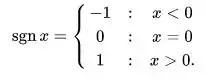 
Logo, f’(x) será igual a 0 em todos os três casos, pois trata-se de derivada de uma constante.
Passo 2
Sendo assim, o limite da função derivada a direita de zero será:
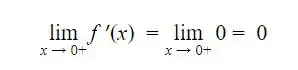
Passo 3
Já o limite da função derivada à esquerda de zero será:
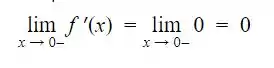
Assim, 
.
Resposta
Demonstração.
Exercícios de Livros Relacionados
Os gráficos de uma função f e sua derivada f ' são mostrando. Qual é maior, f ' ( - 1 ) ou f ' ' ( 1 ) ?
O gráfico de f é dado. Declare, com razões, os números em que f não é diferenciável.
O gráfico de f é dado. Declare, com razões, os números em que f não é diferenciável.
Os gráficos de uma função f e sua derivada f ' são mostrando. Qual é maior, f ' ( - 1 ) ou f ' ' ( 1 ) ?
O gráfico de f é dado. Declare, com razões, os números em que f não é diferenciável.