40) Dada f x = x 3 . Use uma calculadora para tabular valores de f 2 + ∆ x - f ( 2 ) ∆ x quando ∆ xé1 ,0,5 ,0,1 ,0,01 ,0,001 , e∆ xé - 1 ,- 0,5 ,- 0,1 ,- 0,01 ,- 0,001 é é . A que f 2 + ∆ x - f ( 2 ) ∆ x parece tender quando ∆ x aproxima-se de 0?Ache f ' (2) aplicando a fórmula (4).Use uma calculadora para tabular valores de f x - f ( 3 ) x - 3 quando xé3 ,2,5 ,2,1 ,2,01 ,2,001exé1 ,1,5 ,1,9 ,1,99 ,1,9999 é é . A que f x - f ( 3 ) x - 3 parece tender quando ∆ x aproxima-se de 3?Ache f ' (2) aplicando a fórmula (7).

f 2 + ∆ x - f ( 2 ) ∆ x parece tender a 12 quando ∆ x aproxima-se de 0. f ' 2 = 12 f x - f ( 2 ) x - 2 parece tender a 12 quando x aproxima-se de 2. f ' 2 = 12

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 3.1 - Ex. 40

40) Dada .

Use uma calculadora para tabular valores de quando . A que parece tender quando aproxima-se de 0?

Ache (2) aplicando a fórmula (4).

Use uma calculadora para tabular valores de quando . A que parece tender quando aproxima-se de 3?

Ache (2) aplicando a fórmula (7).

Passo 1

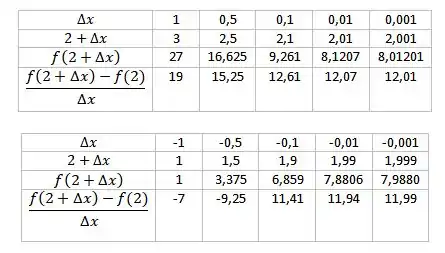
Concluímos então que, parece tender a 12 quando aproxima-se de 0.

Passo 2

A fórmula (4) solicitada na questão é:

Assumindo que , temos:

Logo, aplicando na definição:

Desenvolvendo o produto notável e simplificando, temos:

Passo 3

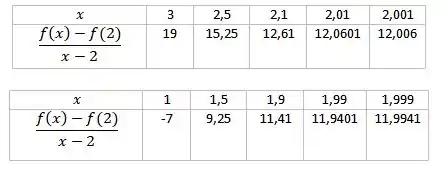
Concluímos então que, parece tender a 12 quando aproxima-se de 2.

Passo 4

A fórmula (7) solicitada na questão é:

Assumindo que , temos:

Logo, aplicando na definição:

Desenvolvendo o produto notável, temos:

Simplificando, teremos:

Resposta

parece tender a 12 quando aproxima-se de 0.
parece tender a 12 quando aproxima-se de 2.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta.Se a reta tangente ao gráfico de y = f x em x = - 2 tiver inclinação negativa, então f ' - 20 .

Seja f x = 2 x , obtenha uma estimativa de f ' 1 pelos seguintes métodos:Usando um recurso gráfico para fazer um zoom em um ponto apropriado do gráfico até que ele se pareça a uma reta e, então, estim

Esboce o gráfico da derivada da função cujo gráfico é dado.

Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta.Se uma curva y = f x tiver uma reta tangente horizontal em x = a , então f ' a não está definida.

A função f cujo gráfico aparece abaixo tem valores dados na tabela a seguir.Use os dados da tabela para calcular os quocientes de diferenças f 3 - f 1 3 - 1 , f 2 - f 1 2 - 1 , f 2 - f 0 2 - 0 Usando