Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 2.2 - Ex. 37

Seja f x = 2 x , obtenha uma estimativa de f ' 1 pelos seguintes métodos:

  1. Usando um recurso gráfico para fazer um zoom em um ponto apropriado do gráfico até que ele se pareça a uma reta e, então, estimando a inclinação.
  2. Usando um recurso gráfico para estimar o limite na fórmula 13 , fazendo uma tabela para uma sucessão de valores de w tendendo a 1 .

Passo 1

  1. Vamos ver o gráfico de f x = 2 x :

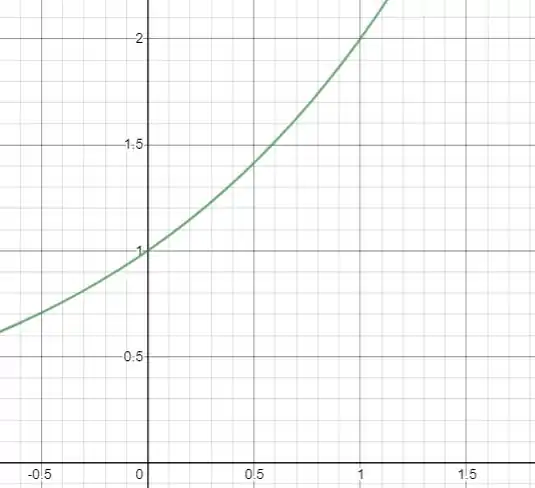
    2. Vamos estimar a reta tangente em x = 1 usando os pontos 1,2 e 0,6 ; 1,5 :

    m = f x - f x 0 x - x 0

    Usando x , f x = 1 , 2 e x 0 , f x 0 = 0 , 5 7 ; 1 , 5 e substituindo:

    m = f x - f x 0 x - x 0 = 2 - 1 , 5 1 - 0 , 6 = 0 , 5 0,4 = 5 4 = 1,25

    Passo 2

  2. Vamos estimar o limite:

f ' x = lim w → x ⁡ f w - f x w - x

Fazendo uma tabela para uma sucessão de valores de w tendendo a 1 nós temos:

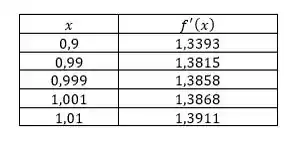
Vemos que o limite em 1 tende a 1,38 .

Resposta

  1. 1,25
  2. 1,38
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a fórmula para a derivada em relação a x de sec ⁡ x c o s s e cx c o t gx
Coeficientes angulares no gráfico da função cotangente: Esboce em apenas um gráfico y = c o t g( x ) e sua derivada em 0xπ . O gráfico da função cotangente parece ter um coeficiente angular mínimo? E
Coeficientes angulares no gráfico da função tangente: Esboce em apenas um gráfico y = t g( x ) e sua derivada em ( - π / 2 ,π / 2 ) . O gráfico da função tangente parece ter um coeficiente angular mín
Explorando ( s e nk x ) / x : Esboce em um único gráfico y = ( s e nx ) / x , y = ( s e n2 x ) / x e y = ( s e n4 x ) / x no intervalo - 2 ≤ x ≤ 2 . Onde cada gráfico parece cruzar o eixo y ? Os gráfi
Radianos versus graus: derivadas no modo grau. O que aconteceria com as derivadas de sen ⁡ x e cos ⁡ x se x fosse medido em graus em vez de radianos? Para descobrir isso, siga os seguintes passos:Sele