Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 2.2 - Ex. 25
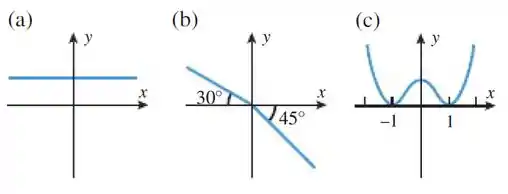
Esboce o gráfico da derivada da função cujo gráfico é dado.
Passo 1
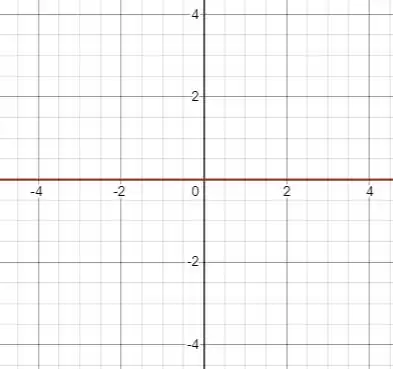
Na função da letra a) é constante, e sabemos que a derivada é igual a zero para todo real, assim abaixo temos o gráfico:
Passo 2
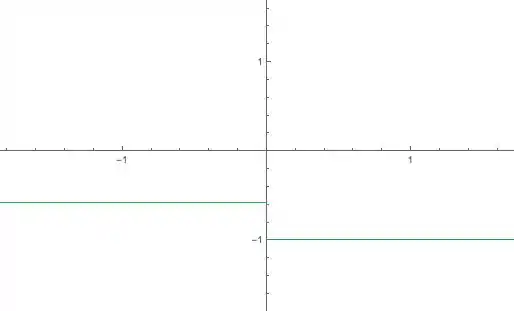
Já a função da letra b) temos duas inclinações diferentes, uma para e outra para . Como as inclinações são das retas tangente, podemos achar elas pela expressão da tangente dos ângulos:
Assim podemos esboçar o gráfico da derivada:
Passo 3
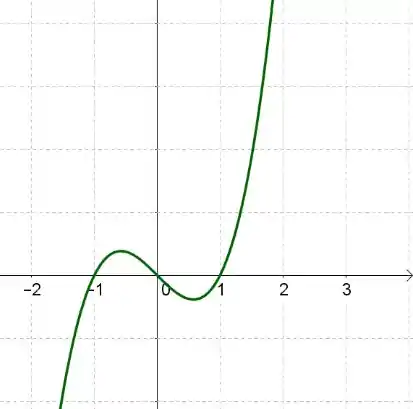
E por último, a função da letra c) vemos que em , e as retas tangentes são horizontais, assim as derivadas nesses pontos são iguais a zero.
E quando aumenta, a partir de , a inclinação da reta tangente cresce, e quando dominui, em , a inclinação da reta tangente diminui.
Vamos então esboçar o gráfico da derivada:
Resposta
Ei, a resposta está no passo a passo :)