Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 0.4 - Ex. 35

Dado que θ = arc tg ⁡ 4 3 , encontre os valores exatos de sen ⁡ θ , cos ⁡ θ , cotg ⁡ θ , sec ⁡ θ e cossec ⁡ θ .

Passo 1

Fala galera, tudo tranquilo? Vamos bater um papo sobre trigonométricas inversas ok? Se:

θ = arc tg ⁡ 4 3

Então θ é o arco cuja tangente é 4 3 . Fazendo a inversa da inversa, temos:

tg ⁡ θ = 4 3

Ao invés de tentar achar θ pra usar dentro de sen ⁡ θ , cos ⁡ θ , cotg ⁡ θ , sec ⁡ θ e cossec ⁡ θ , podemos aproveitar essa info pra montar um triângulo auxiliar bacana:

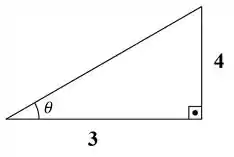
Dessa forma, confirmamos o valor exato da tangente em! E por Pitágoras, achamos a hipotenusa:

H 2 = 3 2 + 4 2

H 2 = 9 + 16

H 2 = 25

H = 5

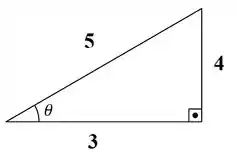
Passo 2

Agora galera, a gente mete bronca usando o triângulo auxiliar, ok? Seja:

sen ⁡ θ = c a t e t o   o p o s t o h i p o t e n u s a

cos ⁡ θ = c a t e t o   a d j a c e n t e h i p o t e n u s a

cotg ⁡ θ = 1 tg ⁡ θ

sec ⁡ θ = 1 cos ⁡ θ

cossec ⁡ θ = 1 sen ⁡ θ

Vamos ter:

sen ⁡ θ = 4 5

cos ⁡ θ = 3 5

cotg ⁡ θ = 3 4

sec ⁡ θ = 5 3

cossec ⁡ θ = 5 4

Resposta

sen ⁡ θ = 4 5

cos ⁡ θ = 3 5

cotg ⁡ θ = 3 4

sec ⁡ θ = 5 3

cossec ⁡ θ = 5 4

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A função f x = e x + x , sendo derivável e injetora, tem uma inversa derivável f - 1 x . Determine o valor de d f - 1 / d x no ponto f ( ln ⁡ 2 ) .
Determine a inversa da função f x = 1 + 1 x , x ≠ 0 . Em seguida, mostre que f - 1 f x = f f - 1 x = x e que d f - 1 d x ​ f x = 1 f ' x .
O que é uma função um a um?A partir do gráfico, como dizer se uma função é um a um?
Use um gráfico para decidir se f é um a um. f x = x 3 + x
Use um gráfico para decidir se f é um a um. f x = x 3 - x