Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 8.1 - Ex. 7e
Dado que , ache o valor exato de cada uma das funções:
7. e)
Passo 1
Temos que mexer primeiro o valor da função inversa do seno, que é o nosso . Aí partimos para a cossecante e matamos a questão, ok?
Passo 2
Temos a definição que diz que se. Queremos o valor de e temos o , que é , certo?
se
Só substitui o valor de na definição.
Passo 3
Agora, vamos lembrar do triângulo retângulo, segue o raciocínio...
, então o cateto oposto é 1 e a hipotenusa é 3, foi?
Por Pitágoras, calculamos o cateto adjacente, que será... , vamos usar essa info mais pra frente
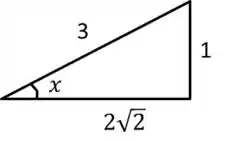
Passo 4
Bem, se sabemos quem são , os catetos e a hipotenusa, agora podemos calcular o que o item pede, .
Como sabemos... , então:
Tranquilo, né?
Resposta
Exercícios de Livros Relacionados
Nos Exercícios 53 e 54, resolva em k .54. c) e ln 0,8 k = 0,8
Nos Exercícios 47-52, resolva y em função de t ou x , conforme for apropriado.47. ln y = 2 t + 4
Use as propriedades dos logaritmos para simplificar as expressões nos Exercícios 41 e 42.42. c) 3 ln t 2 - 1 3 - l n ( t + 1 )
Determine expressões mais simples para as quantidades nos Exercícios 43-46.44. a) e l n ( x 2 + y 2 )
Use as propriedades dos logaritmos para simplificar as expressões nos Exercícios 41 e 42.41. b) ln 3 x 2 - 9 x + ln 1 3 x