Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 1.1 - Ex. 3 e
O gráfico de uma função é dado:
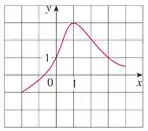
e) Diga qual é o domínio e a imagem de .
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado nos deu o gráfico de uma função e pediu pra gente encontrar o domínio e a imagem dela.
Sabendo que o domínio de uma função são todos os valores que a variável assume. E a imagem são todos os valores que, ou seja, a função, assume.
Então é só olharmos os valores que aparecem no gráfico da função, analisando os intervalos de e .
Vamos lá!
Passo 2
Vamos começar analisando nosso gráfico, olhando os intervalos de e nos quais nossa função é definida, ou seja, onde a curva é contínua no gráfico:
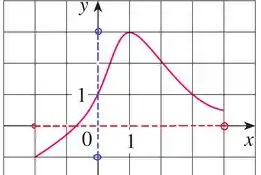
Observe que o menor valor de onde a função está contida é e que o maior valor de é . Então, o domínio da nossa função está definida no intervalo:
Agora observe que o menor valor de para o qual a nossa função tem um correspondente em e está definida é e o maior valor é . Então, nossa imagem é dada por:
Prontinho, galera! Até a próxima! 😉