Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 4.3 - Ex. 7
Em cada item, indique as coordenadas x dos pontos de inflexão de f. Dê razões para suas escolhas.
(a) Esta curva é o gráfico de f.
(b) Esta curva é o gráfico de .
(c) Esta curva é o gráfico de .
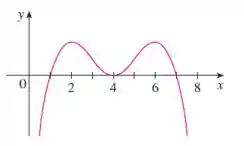
Passo 1
Eaee, belezinha?? Bom... a questão nos dá o seguinte gráfico de uma função:
A questão quer que indiquemos as coordenadas dos pontos de inflexão se esse gráfico for de uma função , ou .
Bom... Algumas vezes na nossa vida chegamos a um ponto que sentimos que temos que mudar algo, né não? Na matemática também acontece. Assim é o ponto de inflexão, onde a concavidade se revolta e muda de direção hehe.
Então bora lá!! 😉
Passo 2
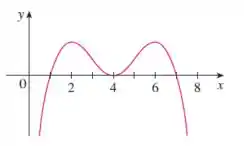
Analisando o gráfico de :
O ponto de inflexão é em pois a concavidade muda de baixo para cima.
E também em , onde a concavidade muda de cima para baixo.
Passo 3
Para o gráfico de , temos que a concavidade é para baixo se a primeira derivada for decrescente e a concavidade é para cima se a primeira derivada for crescente.
Dessa forma, os pontos onde há uma mudança de concavidade, ou seja, pontos de inflexão, são aqueles onde a primeira derivada chega nos seus pontos máximos ou mínimos, pois são neles que a curva deixa de ser crescente e passa a ser decrescente ou vice-versa.
Pelo gráfico vemos que esses pontos ocorrem em (máximos) e em (mínimo).
Passo 4
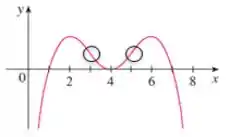
Para o gráfico de , usamos o teste da Segunda Derivada.
Esse teste nos diz que se a segunda derivada for igual a zero e mudar de sinal em um ponto .
Então é um ponto de inflexão.
Isso ocorre pois o sinal da segunda derivada te indica se a concavidade é para cima () ou para baixo ().
Olhando o gráfico vemos que isso ocorre em e em .
Você pode ter pensado também em , afinal a segunda derivada vale zero nesse ponto. No entanto, ela não muda de sinal, ela toca no zero e volta a ser positiva depois, portanto, ali não é um ponto de inflexão.
Resposta
(a) , pois a concavidade muda de baixo para cima. E também em , onde a concavidade muda de cima para baixo.
(b) Para um valor de máximo temos , e em , é um mínimo.
(c) Em e em .