Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.Revisão - Ex. 16
Em (a) a (d), é dado o gráfico completo de um polinômio com grau no máximo 6. Encontre equações para polinômio com grau no máximo 6. Encontre equações para polinômios que produzam gráficos com esses aspectos e verifique suas respostas com um recurso gráfico computacional.
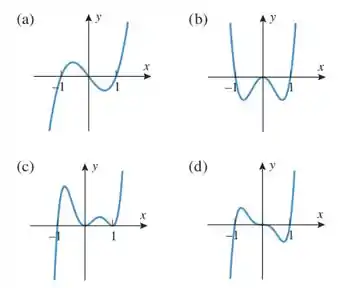
Passo 1
Vamos analisar a função, nos pontos onde a equação encosta no eixo, ou seja na raiz onde .
- A primeira função é dada por:
- A segunda função é dada por:
- A terceira função é dada por:
- A quarta função é dada por:
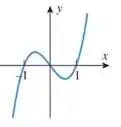
Analisando o gráfico, vemos que a função corta o em 3 pontos, onde:
Isso significa que estamos falando de uma função com 3 raízes.
Para isso, vamos colocar esses pontos em mini funções, onde essas raízes zerem suas próprias funções:
Unindo cada uma dessas “funçõeszinhas” , conseguimos formar uma função maior:
Plotando no gráfico temos:
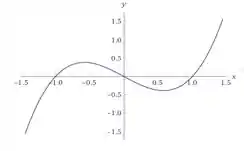
Passo 2
Vamos analisar a função, nos pontos onde a equação encosta no eixo, ou seja na raiz onde .
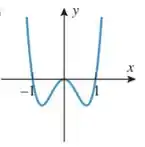
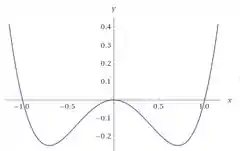
Analisando o gráfico, vemos que a função corta o em 4 pontos, duas vezes no zero e uma vez em 1 e -1, onde:
Isso significa que estamos falando de uma função com 3 raízes.
Para isso, vamos colocar esses pontos em mini funções, onde essas raízes zerem suas próprias funções:
Unindo cada uma dessas “funçõeszinhas” , conseguimos formar uma função maior:
Plotando no gráfico temos:
Passo 3
Vamos analisar a função, nos pontos onde a equação encosta no eixo, ou seja na raiz onde .
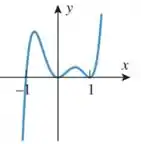
Analisando o gráfico, vemos que a função corta o em 5 pontos, onde temos apenas um ponto tocando em -1, dois pontos direcionados em zero e dois pontos em torno de 1 positivo:
Isso significa que estamos falando de uma função com 5 raízes.
Para isso, vamos colocar esses pontos em mini funções, onde essas raízes zerem suas próprias funções:
Unindo cada uma dessas “funçõeszinhas” , conseguimos formar uma função maior:
Plotando no gráfico temos:
Passo 4
Vamos analisar a função, nos pontos onde a equação encosta no eixo, ou seja na raiz onde .
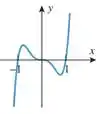
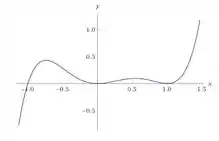
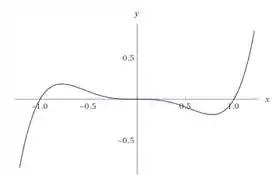
Analisando o gráfico, vemos que a função corta o em 5 pontos, onde se olharmos bem há um ponto encostando em zero e outros dois pontos se proximando pela esquerda e direita, além disso temos outros pontos em -1 e 1:
Isso significa que estamos falando de uma função com 3 raízes.
Para isso, vamos colocar esses pontos em mini funções, onde essas raízes zerem suas próprias funções:
Unindo cada uma dessas “funçõeszinhas” , conseguimos formar uma função maior:
Plotando no gráfico temos:
Resposta
Ei, a resposta está no passo a passo :)